离散系统理论与连续系统理论既有本质的区别,又有极大的相似性。本章的内容就是讨论它们的区别和联系的。本章首先讨论离散信号的数学描述,引入Z变换理论及差分方程,建立线性离散控制系统的数学模型,在此基础上分析离散系统稳定性及计算稳态误差,并分析离散系统的动态性能与数字校正设计。

基本概念

采样和数控技术在自动控制领域中得到了广泛的应用,其主要原因是采样系统,特别是数字控制系统较之相应的连续系统具有如下的特点:
(1)由数字计算机构成的数字校正装置,效果比连续式校正装置好,且由软件实现的控制规律易于改变,控制灵活。
(2)采样信号,特别是数字信号的传递可以有效地抑制噪声,从而提高了系统的抗干扰能力。
(3)允许采用高灵敏度的控制元件,以提高系统的控制精度。
(4)可用一台计算机分时控制若干个系统,提高了设备的利用率,经济性好。
(5)对于具有传输延迟,特别是大延迟的控制系统,可以引入采样的方式稳定。

由于在离散系统中存在脉冲或数字信号,若仍然沿用连续系统中的拉普拉斯变换方法来建立系统各个环节的传递函数,则在运算过程中会出现复变量s的超越函数。为了克服这个障碍，需要采用Z变换法建立离散系统的数学模型。我们将会看到,通过Z变换处理后的离散系统，可以把用于连续系统中的许多方法,如稳定性分析、稳态误差计算、时间响应分析及系统校正方法等,经过适当改变后直接应用于离散系统的分析和设计之中。

信号的采样与保持

将连续信号转变为脉冲信号需要采样器,也称采样开关;而为了控制连续式元件,又需要使用保持器将脉冲信号转变为连续信号。为了定量研究采样系统,必须对信号的采样过程和保持过程用数学方法来加以描述。
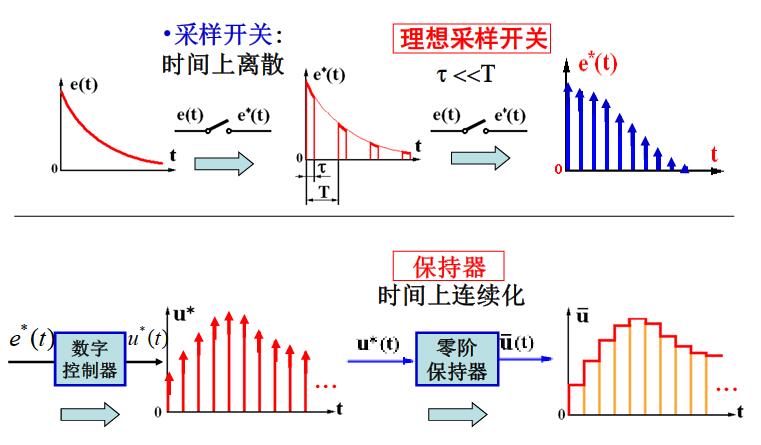
信号的采样与保持

采样过程的数学描述

采样过程就是把连续信号变换成离散信号的过程。采样开关可以看作一个脉冲调制器，这样采样过程就可以看作一个单位脉冲序列δT(t)\delta_T(t)被输入信号e(t)进行幅值调制的过程。

δT(t)=∑n=−∞+∞δ(t−nT)e∗(t)=e(t)δT(t)=e(t)∑n=0+∞δ(t−nT)\delta_T(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT)\\ e^*(t)=e(t)\delta_T(t)=e(t)\sum_{n=0}^{+\infty}\delta(t-nT)\\

在实际采样中，采样开关的闭合时间是τ\tau，导致真正的幅值脉冲序列应当是矩形脉冲序列。于是：

e∗(t)=∑n=0+∞e(t)[1(t−nT)−1(t−nT−τ)]=τ⋅∑n=0+∞e(t)⋅δ(t−nT)\begin{aligned} e^*(t)&=\sum_{n=0}^{+\infty}e(t)[1(t-nT)-1(t-nT-\tau)]\\ &=\tau\cdot\sum_{n=0}^{+\infty}e(t)\cdot\delta(t-nT) \end{aligned}

考虑脉宽τ\tau对系统增益容易产生影响，为了避免它，应当保证采样信号经保持其直接加到后续系统中。大多数的离散控制系统都是这样，所以，通常将此采样开关视作理想采样开关，便可如下书写：

e∗(t)=e(t)⋅∑n=0+∞δ(t−nT)=∑n=0+∞e(nT)⋅δ(t−nT)e^*(t)=e(t)\cdot\sum_{n=0}^{+\infty}\delta(t-nT)=\sum_{n=0}^{+\infty}e(nT)\cdot\delta(t-nT)

香农Shannon采样定理

连续信号采样后变为采样信号，采样信号的信息不等于连续信号的全部信息。可以用频谱分析的方法来探究两类信号之间的相互联系。

频谱，实质是一个时间函数所含不同频率谐波成分的分布情况。

单位脉冲序列δT(t)\delta_T(t)是一个周期函数，所以可以展开为傅里叶函数，并写成复数形式：

δT(t)=1T∑n=−∞+∞ejnwst\delta_T(t)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}e^{jnw_st}

则采样信号可以如下表达，同时，可以对两边进行拉普拉斯变换：

e∗(t)=e(t)δT(t)=1T∑n=−∞+∞e(t)ejnwstE∗(s)=1T∑n=−∞+∞E(s+jnwst)e^*(t)=e(t)\delta_T(t)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}e(t)e^{jnw_st}\\ E^*(s)=\frac{1}{T}\sum_{n=-\infty}^{+\infty}E(s+jnw_st)

令s=jw,则E(jw)为e(t)的频率特性，|E(jw)|为e(t)的幅频特性或称频谱，e(t)的频谱是由最大角频率的。