蒙特卡洛方法/灵敏度分析/正态性检验

🖊️蒙特卡洛方法10.26

[1] Laumakis P J, Harlow G. Structural reliability and Monte Carlo simulation[J]. International Journal of Mathematical Education, 2010, May 01(3): 377-387
[2] 王哲君, 强洪夫, 常新龙, 等. 结构可靠性仿真方法研究[J]. 力学与实践, 2014, 36(1):9-22
原文链接:
[1] http://dx.doi.org/10.1080/00207390210125729
[2] DOI: 10.6052/1000-0879-13-117: http://lxsj.cstam.org.cn/CN/Y2014/V36/I1/9

蒙特卡洛 (Monte-Carlo, MC) 法亦称为概率模拟法，有时也称为随机抽样技术或统计试验方法。 它是一种通过随机变量的统计试验、随机模拟来求解数学物理、工程技术问题近似解的数值方法。 也是最直观、精确、对高度非线性问题最有效的结构可靠性分析方法。

基本MC法

(1)MC 法的理论基础是大数定律。即求解某事件发生的概率时，可通过大量抽样试验的方法，得到该事件出现的频率，将其作为问题的解。
(2) 基本思想：按设计变量的概率密度函数进行大量抽样，用落入失效域的样本点数与总投点数之比作为失效概率的无偏估计值。
(3) 实施步骤：首先根据结构受力、破坏机理，建立极限状态方程；其次对影响可靠度的随机变量进行大量随机样本抽样；然后把这些抽样值一组组地带入极限状态方程，确定失效与否；最后通过统计的方法，依据该方法的基本思想得到失效概率的无偏估计值。

改进MC法

基本 MC 法，通常采用大量投点来提高精度，减小方差。 在失效概率非常小的时候，随机变量落入失效域的几率很小，抽样效率很低，计算量很大。为此需要对基本MC法进行改进，以提高工作效率，尽可能地减少必需的样本量。

优点分析：

通过分析和研究发现，MC 法作为结构可靠性仿真的基本方法，具有非常明显的优点：
(1) MC 法及其程序结构简单，较容易实现；
(2) 只要抽样次数足够多，计算所得的结构可靠度的精度就可满足要求；
(3) 收敛的概率和收敛的速度与基本随机向量的维数、极限状态函数的复杂程度和仿真计算过程无关，无需将状态函数线性化和随机变量当量正态；
(4) 数值模拟的误差也可容易地确定，从而确定模拟的次数和精度。
MC 法是进行结构可靠性仿真的最基本方法，其他仿真计算方法都是以该法为基础，都是针对该方法在计算中出现的问题而提出的。 如何对失效概率较小的结构进行可靠性仿真计算是其面临的主要问题，也是对其进行改进的主要方向。 因此，为在结构可靠性仿真计算中发挥该方法更大的作用，基于控制变数法、等分散抽样法以及支持向量法等新抽样方法仍在不断涌现和发展。 由于 MC 法自身的特点，目前针对特别复杂结构的可靠性分析，一般将基本 MC 法作为检验各种改进方法和新方法有效性的重要手段。

实例：简单吊臂结构

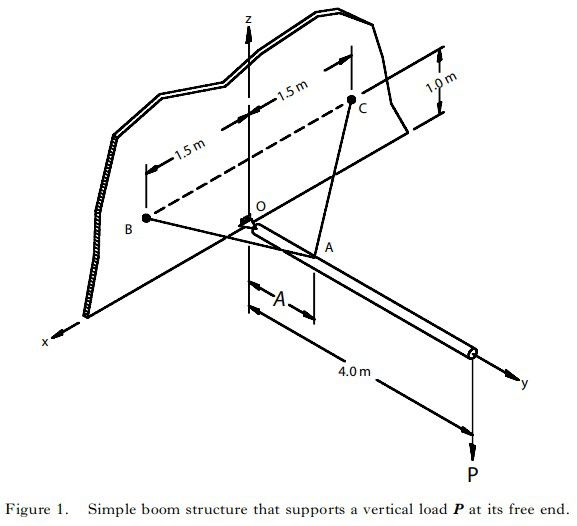
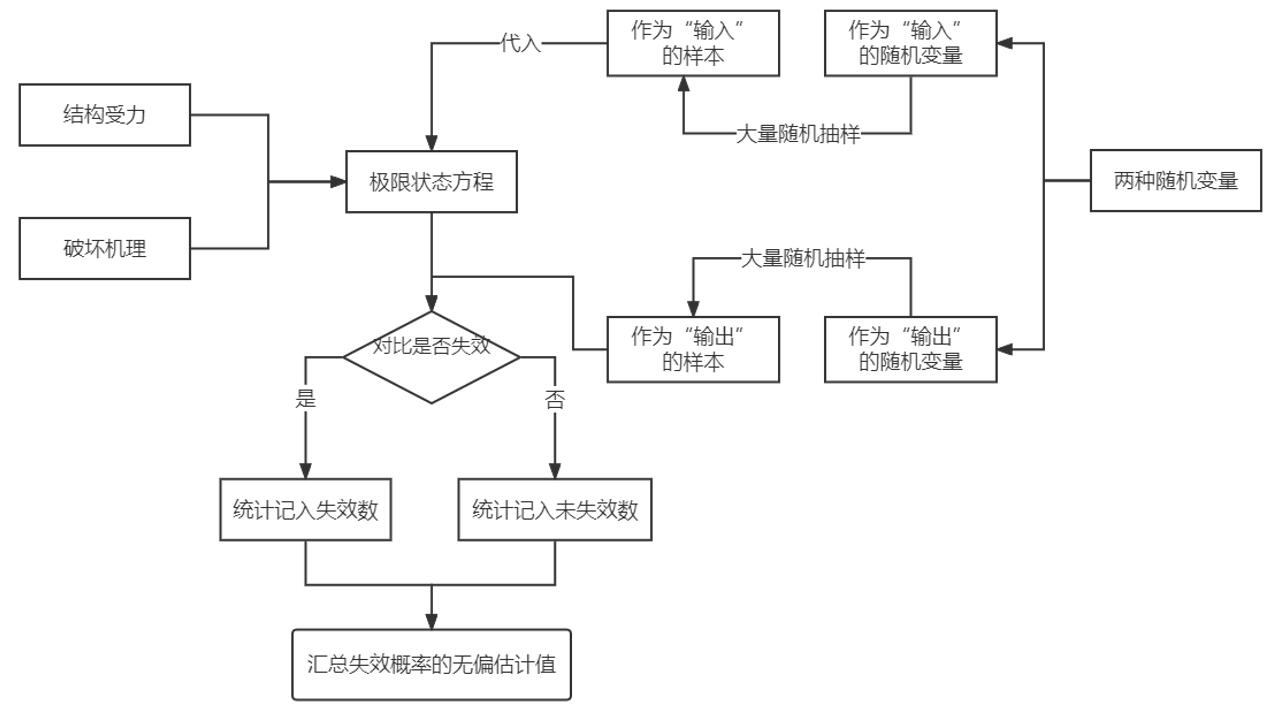
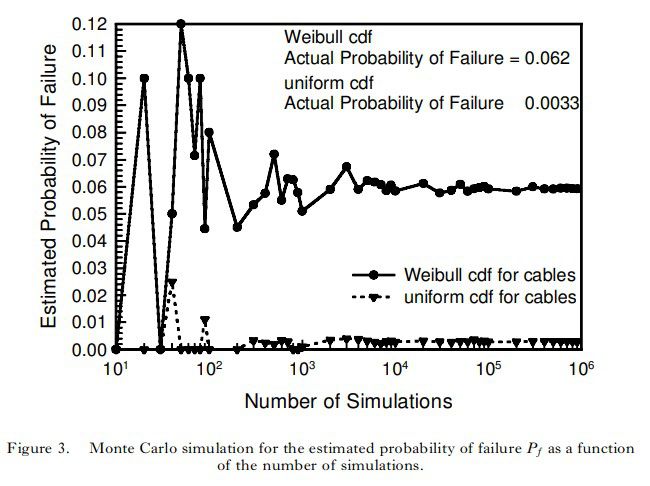
从下图中可以看出，随着抽样数目的不断增大，失效概率逐渐偏向一个稳定值，这背后是符合大数定律的。另一方面，图中两根图线分别对某一随机变量的概率分布函数处理为均匀分布和威布尔分布，这种分布的不同很大程度上会影响最终结果。

✏️灵敏度分析10.27

[1] 杨哲,李曙林,周莉,石晓朋.飞机作战生存力设计参数灵敏度分析[J].北京航空航天大学学报,2013,39(08):1096-1101+1121.DOI:10.13700/j.bh.1001-5965.2013.08.023.
[2] WILKINSON L. Revising the Pareto chart[J]. The American Statistician, 2006, 60(4):332-334.
原文链接:
[1] https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFD2013&filename=BJHK201308020&uniplatform=NZKPT&v=bXj07oiIO7hhXy10_uz0HR2cw8PKNCn5rIYECrzQYn3iRFbWZTrj70DZcZ2AoC9F
[2] DOI: 10.1198/000313006X152243: https://www.tandfonline.com/doi/abs/10.1198/000313006X152243

灵敏度是度量一种因子的变化对另一因子的影响程度，定义方法一般有两种，一种是用模型因变量对模型输入参数的偏导数来表示，即

$$S_i=\frac{\partial y(X)}{\partial x_i}, i=1,2,...,l$$

式中， 为因变量y(X)对参数 的灵敏度，l为模型中参数的个数。
另一种是下式所示的采用灵敏度的标准化无量纲形式：

$$S_i=\frac{\frac{\partial y(X)}{y(X)}}{\frac{\partial x_i}{x_i}}, i=1,2,...,l$$

式（1）为因变量的绝对差值和输入参数绝对差值的比值，其值相当于因变量与输入参数构成的曲线的绝对斜率，适用于比较同一个参数在不同取值时对因变量的影响大小; 公式（2）为因变量输出变化百分比与输入参数变化百分比的比值，其值相当于曲线单位标准化之后的转换斜率，由于为无量纲，因此适用于比较不同参数对因变量的影响大小。
真实计算中，如果无法求因变量关于某一参数的显示灵敏度函数，可以对某一特定参数 取一个微小增量 ，然后用下式近似求解。

$$S_i=\frac{\partial y(X)}{\partial x_i}\approx \frac{y(x_1,x_2,...,x_i+\Delta x_i,...,x_l)-y(x_1,x_2,...,x_i,...,x_l)}{\Delta x_i}, i=1,2,...,l$$

通过灵敏度分析，容易确定对目标因变量影响更大的设计参数，设计优化的重点也将放在这个上面。对于多参数敏感性分析，也可以用下面的公式来比较大小。

$$S_i=\frac{\frac{\partial y(X)}{y(X)}}{\frac{\partial x_i}{x_i}}\approx \frac{\frac{y(x_1,x_2,...,x_i+\Delta x_i,...,x_l)-y(x_1,x_2,...,x_i,...,x_l)}{y(x_1,x_2,...,x_i,...,x_l)}}{\Delta x_i/x_i}, i=1,2,...,l$$

另外，设计参数的取值范围对优化过程和优化结果影响很大。设计参数取值范围过大，则优化效率降低; 若设计参数取值范围过小，则可能造成搜索不到最优解。因此，文献[1]中首先利用公式（3）确定每个参数在一个较大取值范围内的灵敏度，然后选择灵敏度较大的区域作为该优化参数的初始取值范围，进而建立生存力权衡优化设计模型，并 基 于 粒 子 群 优 化 算 法 ( PSO，Particle Swarm Optimization)对其进行优化求解，得出最优设计方案。
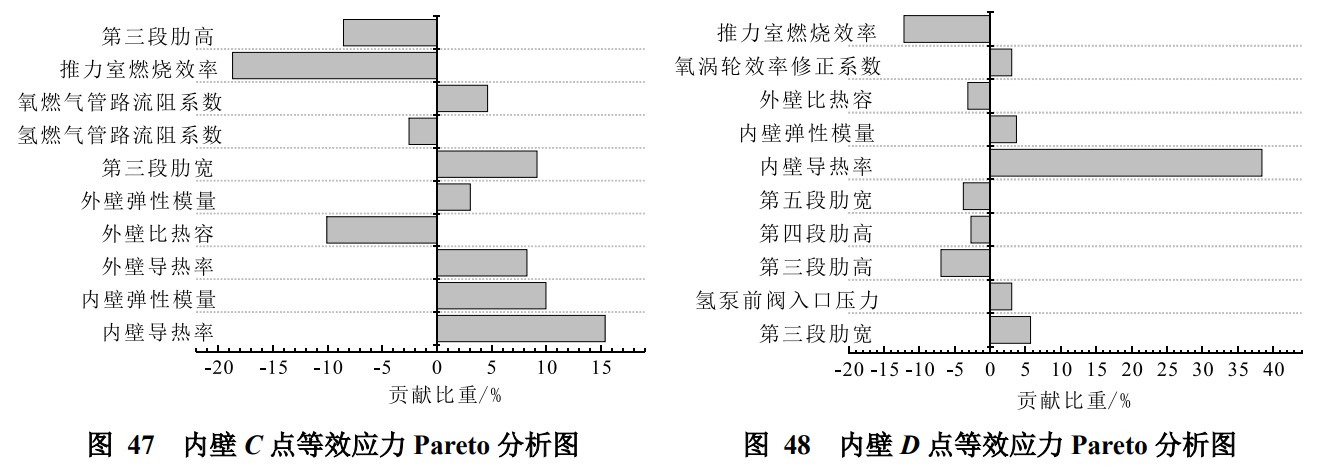
Pareto图在表示批量数据随机抽样的结果上有很好的展示效果。在实践中，针对一组离散因素收集故障频率数据，一般会对这些频率进行分类，并首先解决与最大频率相关的问题。将多参数灵敏度分析的结果用Pareto图进行展示，是比较流行的做法。

🖋️正态性检验10.28

[1] 盛骤. 概率论与数理统计(第五版)[M]. 高等教育出版社，2019.
[2] 假设检验[EB/OL]. 百度百科.2022年04月21日. https://baike.baidu.com/item/假设检验/638320?fr=aladdin
[3] 正态性检验[EB/OL]. 百度百科. 2022年06月16日. https://baike.baidu.com/item/正态性检验/2660263?fr=aladdin
[4] 关于偏度与峰度的一些探索[EB/OL]. 搜狐. 2017年02月05日. https://www.sohu.com/a/125526669_609133
[5] 田禹. 基于偏度和峰度的正态性检验[D].上海交通大学,2012.
[6] 非参数正态性检验[D]. CSDN. 2021年06月25日. https://blog.csdn.net/qq_42722197/article/details/118215010
[7] 张领科,董家强.弹道一致性评定中的样本顺次正态性检验[J].火炮发射与控制学报,2015,36(02):68-72.DOI:10.19323/j.issn.1673-6524.2015.02.015.

假设检验

假设检验(hypothesis testing)，又称统计假设检验，是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。显著性检验是假设检验中最常用的一种方法，也是一种最基本的统计推断形式，其基本原理是先对总体的特征做出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受做出推断。
一般来说，假设检验问题会表述为在某一显著性水平$\alpha$下，检验假设:

$$H_0：\mu=\mu_0,H_1：\mu\not ={\mu_0}$$

其中$H_0$称为原假设或零假设，$H_1$称为备择假设（意指在原假设被拒绝后可供选择的假设）。检验法则是根据样本作出的，总有可能做出错误的决策。在假设$H_0$实际上为真时，我们可能犯拒绝$H_0$的错误，称这类“弃真”的错误为第Ⅰ类错误；在假设$H_0$实际上不真时，我们可能犯接受$H_0$的错误，称这类“取伪”的错误为第Ⅱ类错误。
对于只控制第Ⅰ类错误的概率，而不考虑第Ⅱ类错误的概率的检验，称为显著性检验，一般广泛采用这种检验方法。第Ⅰ类错误的检验法则可以表示为：

$$P(当H_0为真时拒绝H_0)\leq\alpha$$

依据研究的问题不同，会设置一个检验统计量，依据检验统计量来确定拒绝域，拒绝域的边界点称为临界点。
假设检验的基本思想是“小概率事件”原理，其统计推断方法是带有某种概率性质的反证法。小概率在数值上具体指多小，就由显著性水平$\alpha$来表征。

正态性检验

利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。常用的正态性检验方法有正态概率纸法、夏皮罗-威尔克检验法(Shapiro-Wilk test)，科尔莫戈罗夫检验法，偏度-峰度检验法等。
对总体 ，正态性检验问题为：

$$H_0：总体X服从正态分布,H_1：总体X不服从正态分布$$

偏度-峰度检验法

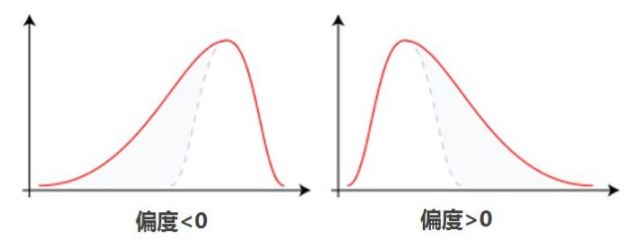
偏度（Skewness）衡量随机变量概率分布的不对称性，是相对于平均值不对称程度的度量，通过对偏度系数的测量，我们能够判定数据分布的不对称程度以及方向。
具体来说，对于随机变量X，我们定义偏度为其的三阶标准中心距：

$$Skew(X)=E[(\frac{X-\mu}{\sigma})^3]=\frac{E[(X-\mu)^3]}{(E[(X-\mu)^2])^{3/2}}$$

对于样本x的偏度SK，基于矩估计可以表示为：

$$SK=\frac{\frac{1}{n}\sum\limits_{i=1}^{n}(x_i-\bar{x})^3}{(\frac{1}{n}\sum\limits_{i=1}^{n}(x_i-\bar{x})^2)^{3/2}}$$

偏度为正，分布右偏；偏度为负，分布左偏。注意，样本分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置。正态分布的偏度应当为0。值得注意的是，SK表达式的计算结果是对偏度的有偏估计。

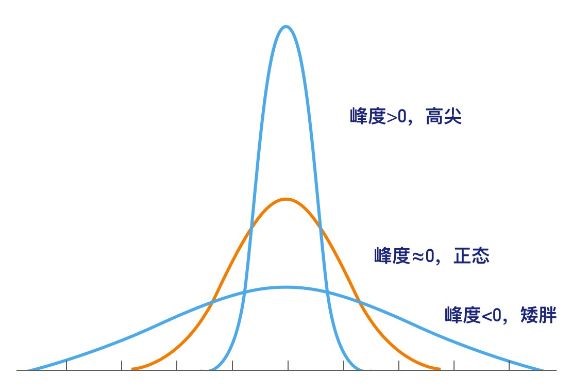
峰度（Kurtosis）是研究数据分布陡峭或平滑的统计量，通过对峰度系数的测量，我们能够判定数据相对于正态分布而言是更陡峭还是平缓。
对于随机变量X，我们定义峰度为四阶中心距除以方差的平方减三：

$$\gamma_2(X)=E[\frac{(X-\mu)^4}{\sigma^2}]-3=\frac{E[(X-\mu)^4]}{(E[(X-\mu)^2])^2}-3$$

对于样本x的峰度K，基于矩估计可以表示为：

$$K=\frac{\frac{1}{n}\sum\limits_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum\limits_{i=1}^{n}(x_i-\bar{x})^2)^2}-3$$

当峰度约等于0时，可认为分布近似服从正态分布；当峰度大于0时，尖峰分布；当峰度小于0时，扁平分布。另外，K表达式的计算结果对峰度也是有偏估计。

偏度-峰度正态性检验又可以分为偏度检验、峰度检验以及偏度和峰度联合检验。三种方法以偏度和峰度为基础，分别采用了不同的正态性检验统计量。基于该统计量的一个新统计量（具体见文献[5]）的极限分布符合标准正态分布或卡方分布，可以借此容易地得到拒绝域。
也有资料显示，在SPSS等统计分析软件中，会计算峰度和偏度的Z评分来帮助检验。

图示法：P-P图和Q-Q图

P-P图反映了变量的实际累积概率与理论累积概率的符合程度，Q-Q图反映了变量的实际分布与理论分布的符合程度，两者意义相似，都可以用来考察数据资料是否服从某种分布类型。若数据服从正态分布，则数据点应与理论直线（即对角线）基本重合。

非参数检验方法

正态性检验属于非参数检验，原假设为“样本来自的总体与正态分布无显著性差异，即符合正态分布”。
通常SPSS软件采用的非参数检验方法有两种，一种是Shapiro-Wilk检验，适用于小样本资料（SPSS规定样本量≤5000），另一种是Kolmogorov–Smirnov检验，适用于大样本资料（SPSS规定样本量>5000）。它们都是通过比较样本经验分布函数与给定分布函数来推断该样本是否来自给定分布函数的总体[6]。

Epps-Pulley检验法

张晟的原论文中采用的正态性检验方法即是Epps-Pulley检验，它是基于经验特征函数的一个无方向正态性检验方法，对多种被择假设都有较高的功效。检验统计量为：

$$W_{EP}=1+\frac{n}{\sqrt{3}}+A-B$$

这里不再对相关参数作详解。当样本容量不同时，检验统计量也会稍有不同。同时该方法的提出者TW Epps和LB Pulley已经根据显著性水平和样本容量给出了一系列临界值，只需要将样本带入上公式再和刚才的临界值比较即可判断正态性。
私认为这也是参数检验方法的一种，本质应该（？）是多阶样本矩的变种。对比传统方法，该方法的优势应当是体现在计算上更方便。