2/6 控制系统的数学模型（上）

引言

描述控制系统的输入变量、输出变量以及内部变量之间动态关系的数学表达式就称为数学模型。数学模型，是对系统进行定量分析和设计的基础。
（1）同一系统，由于描述方法或研究方法的不同，可以采用不同的数学模型。
（2）不同的系统也可以由完全相同的数学模型来表示。

建立数学模型可以通过：

1. 分析法：分析系统各部分的运动机理，根据它们依据的物理规律、化学规律等列些运动方程。
2. 实验法：实验法所建立的模型未必能描述系统内部的运行机理，但能描述输入量与输出量之间的动态关系。 这也称为系统辨识方法。
   • 人为地给系统输入端施加某种测试信号，记录其输出响应；
   • 根据记录的输入、输出数据，用适当的数学模型去逼近黑箱，从而建立数学模型。

时域数学模型（微分方程）

控制系统的微分方程

用解析法列写微分方程的一般步骤：

1. 根据系统或元件的具体工作情况，确定系统或元件的输入、输出变量。
2. 从输入端开始，按照信号的传递顺序，依据各变量所遵循的物理（或化学）规律，列写出系统各元部件的动态方程，一般为微分方程组。
3. 消去中间变量。写出输入、输出变量的微分方程。
4. 将微分方程标准化，即将与输入有关的各项放在等号右侧，与输出有关的各项放在等号左侧，并按降幂排列。且输出量$c(t)$前面的系数为1，方程中除了输入量和输出量及其各阶导数之外。其他各量都是系统已知的结构参数。

相似系统揭示了不同物理现象间的相似关系，可以使设计人员将对一个系统的分析结果推广到具有相同微分方程模型的其他系统。也为控制系统的计算机仿真提供了基础。

控制系统的线性近似

用线性微分方程描述的系统称为线性系统。若线性微分方程的系数是常数称为线性定常系统；若线性微分方程的系数是时间的函数叫线性时变系统。

线性系统的重要性质：叠加原理=齐次性+可加性

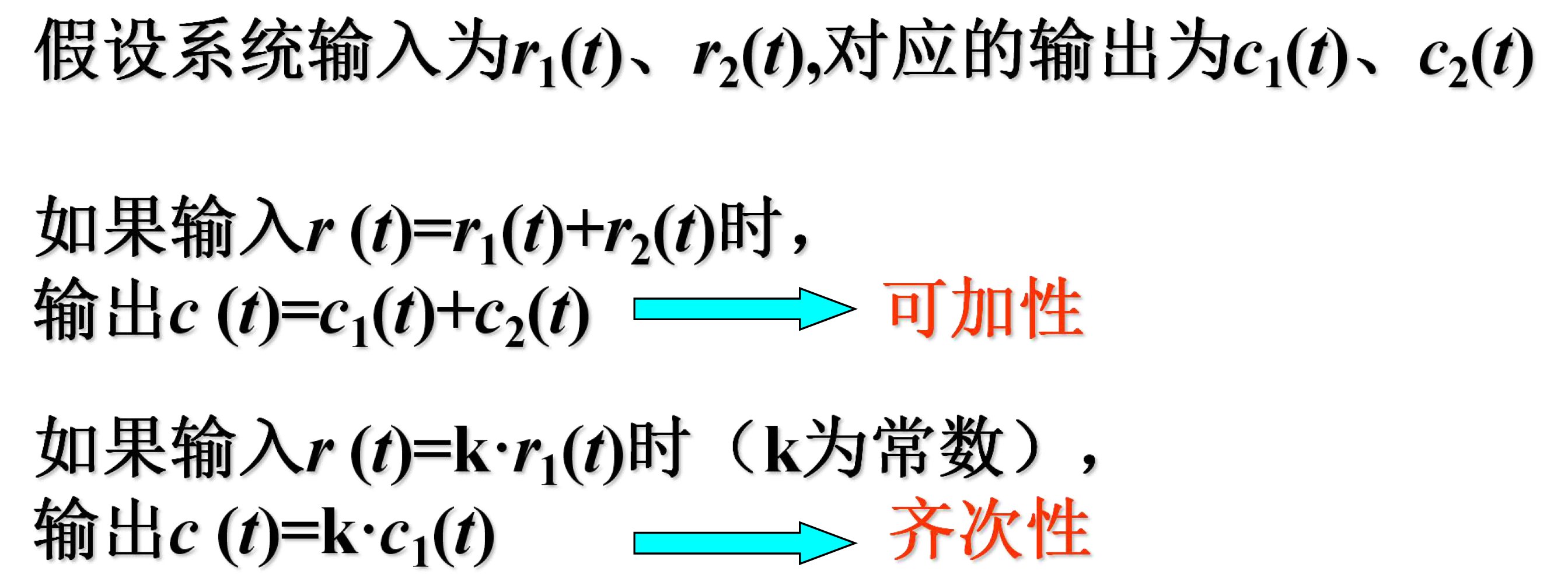
线性系统的叠加原理表明，多个外作用同时作用于系统所产生的总输出，等于各个外作用单独作用时分别产生的输出之和，且外作用的数值增大若干倍时，其输出亦增大相同的倍数。因此，对线性系统进行分析和设计时。如果有几个外作用同时作用于系统，则可以将它们分别处理，依次求出各个外作用单独作用时系统的输出。然后将它们叠加，每个外作用在数值上可以只取单位值，从而大大简化了线性系统的研究工作。

事实上，任何一个元件或系统总是存在一定程度的非线性。将非线性微分方程线性化的方法主要有两种：

1. 忽略弱非线性因素。如果元件的非线性因素较弱或者不在系统非线性工作范闱以内。则它们对系统的影响很小。就可以忽略。
2. 小偏差法（切线法、增量线性化法）。小偏差法基于一种假设，就是在控制系统的整个调节过程中。各个元件的输入量和输出量:只是在平衡点附近作微小变化。这一假设是符合许多控制系统实际工作情况的。因为对闭环控制系统而言。一有偏差就产生控制作用，来减小或消除偏差，所以各元件只能工作在平衡点附近。

小偏差法

假设控制系统中某非线性函数f(x)在平衡点(x0，y0)处连续可微。则可将f(x)在平衡点附近展开成泰勒级数：

$$y=f(x)=y_0+\frac{dy}{dx}\vert _{x_0}(x-x_0)+\frac{1}{2!}\frac{d^2y}{dx^2}\vert _{x_0}(x-x_0)^2+\cdots$$

当（x-x0）很小时，忽略二次以上的各项，上式可以写成：

$$y-y_0=\frac{dy}{dx}\vert _{x_0}(x-x_0)$$

在平衡点附近的小范围内用线性代替非线性。

$$\varDelta y=K\varDelta x, K=\frac{dy}{dx}\vert _{x_0}$$

忽略增量符号，即平衡点附近的线性方程(切线)为：

$$y=Kx$$

请注意:
1）小偏差线性化法只是在平衡点附近有效。
2）控制系统的大多数工作状态是适用小偏差法的。因为对闭环控制系统而言，一有偏差就产生控制作用，来减小或消除偏差，所以各元件一般都工作在平衡点附近。
3）小偏差线性化方法适用于在平衡点处可以泰勒展开的非线性系统，不适用于某些本质非线性的系统。

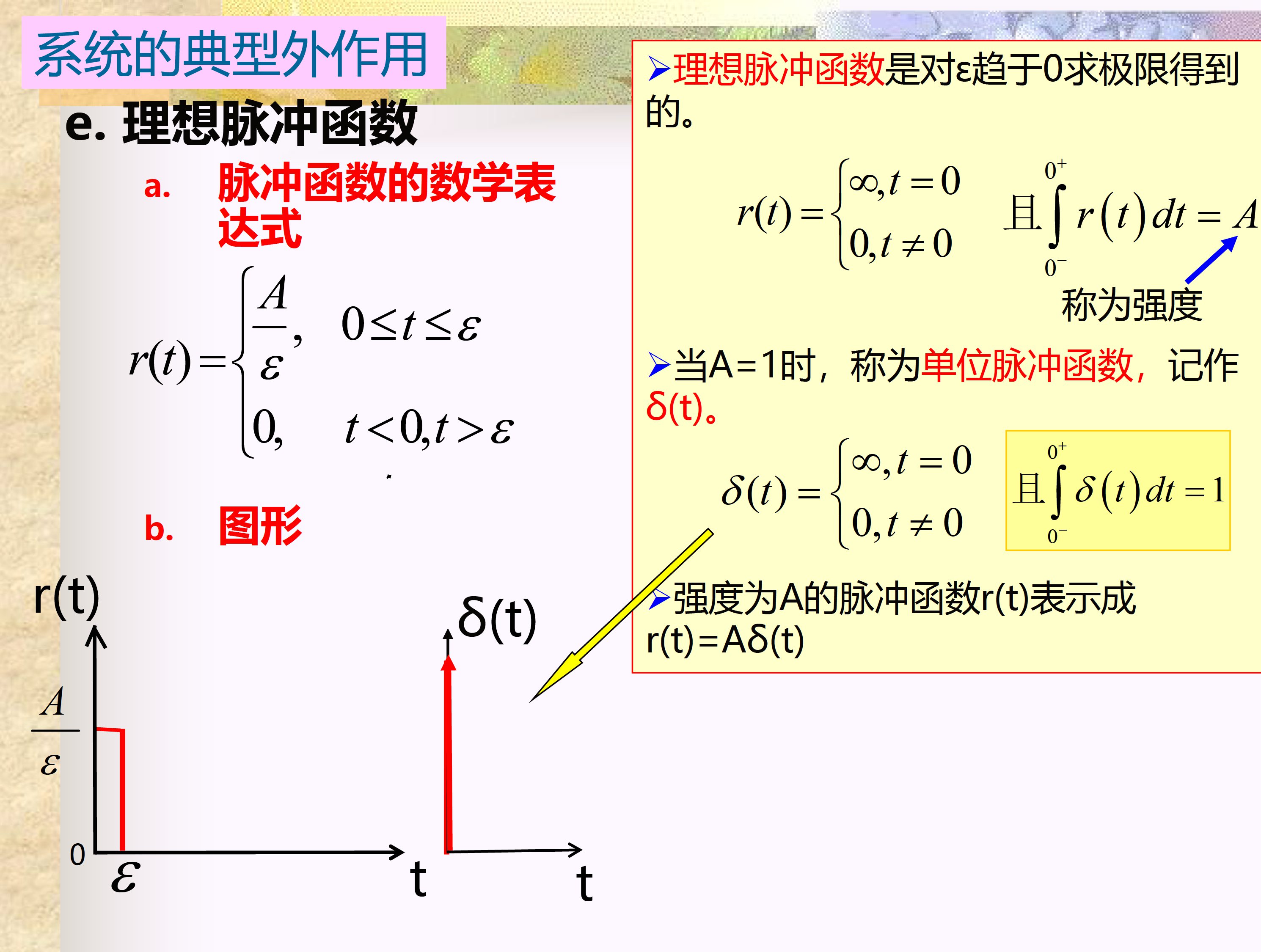
最后简单介绍脉冲函数：

拉普拉斯变换与微分方程的求解

拉普拉斯变换是一种积分变换。它可将时间域内的微分方程变换成复数域内的代数方程。并在变换时引入了初始条件，可以方便地求解线性定常系统的微分方程；同时。拉普拉斯变换也是建立系统复数域的数学模型—— 传递函数的数学基础。

定义

定义：设函数f(t)当t≥0（非常重要！)时有定义，而且积分

$$F(s)=\int_0^\infty f(t)e^{-st}dt$$

存在，则称$F(s)$是$f(t)$的拉普拉斯变换，记作$F(s)=L[f(t)]$，其中，$s$是复变量。$F(s)$称为时间域内的函数$f(t)$的象函数，$f(t)$称为$F(s)$的原函数。例如，针对$f(t)=A⋅1(t)$，有原函数：

$$F(s)=\int_0^\infty A\cdot 1(t)e^{-st}dt=\int_0^\infty Ae^{-st}dt=-\frac{A}{s}e^{-st}\vert _0^\infty =\frac{A}{s}$$

拉氏变换的性质

1. 线性性质：原函数和的拉氏变换等于各原函数的拉氏变换之和

$$L[af_1(t)+bf_2(t)]=aL[f_1(t)]+bL[f_2(t)]=aF_1(s)+bF_2(s)$$

2. 微分性质（可用分部积分法求解）:
   
3. 积分性质：
   
4. 初值定理：原函数的初值等于其象函数乘以s的终值

$$\lim_{t\rightarrow 0}f(t)=\lim_{s\rightarrow\infty}sF(s)$$

5. 终值定理：原函数的终值等于及象函数乘以s的初值

$$\lim_{t\rightarrow\infty}f(t)=\lim_{s\rightarrow 0}sF(s)$$

6. 位移定理
   • 实域中的位移定理：若原函数在时间上延迟τ，则其象函数应乘以$e^{-τs}$

   $$L[f(t-\tau)\cdot 1(t-\tau)]=e^{-\tau\cdot s}F(s)$$

   • 复域中的位移定理：若象函数的自变量延迟a，则原函数应乘以$e^{at}$

   $$L[e^{at}f(t)]=F(s-a)$$

应当用上述若干定理，去理解记忆下面的常用拉氏变换规律。

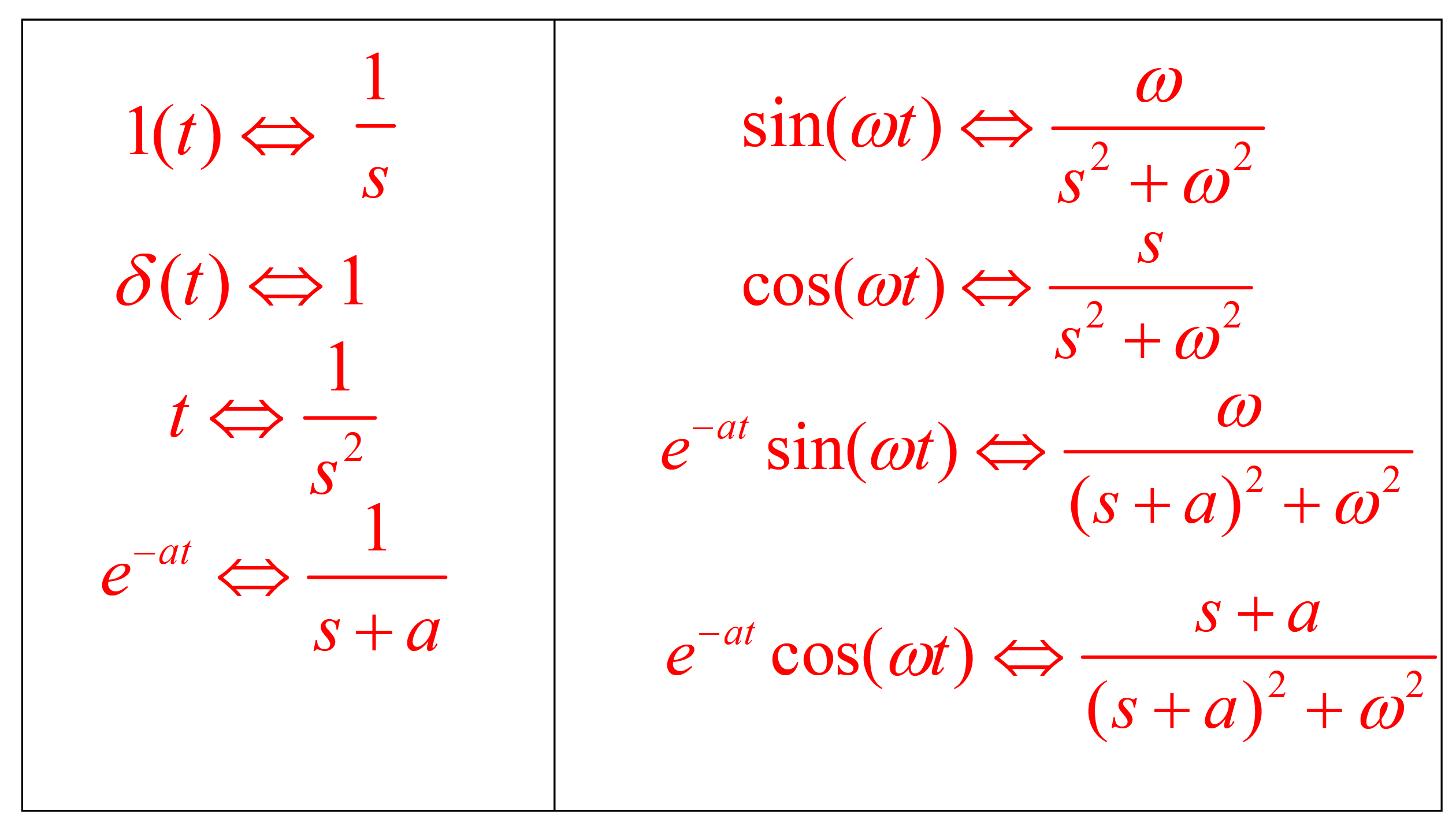
拉普拉斯反变换

由象函数F(s)求原函数f(t)的运算称为拉氏反变换，记为$L^{-1}[F(s)]=f(t)$。由于直接按定义求原函数太复杂，一般都用查拉氏变换表的方法求拉氏反变换。
在控制系统中遇到的象函数，多为如下有理分式形式，即

$$F(s)=\frac{B(s)}{A(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{a_ns^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}(n>m)$$

可以令A(s)=0，此后分情况讨论：

A(s)=0无重根

这时，F(s)可展开为n个简单的部分分式之和的形式，即

$$F(s)=\frac{c_1}{s-s_1}+\frac{c_2}{s-s_2}+\cdots+\frac{c_n}{s-s_n}=\sum_{i=1}^n\frac{c_i}{s-s_i}$$

$s_i$是方程A(s)=0的根，对应的$c_i$为F(s)在$s_i$处的留数，可以根据下式子计算：

$$c_i=\lim_{x\rightarrow s_i}(s-s_i)F(s)$$

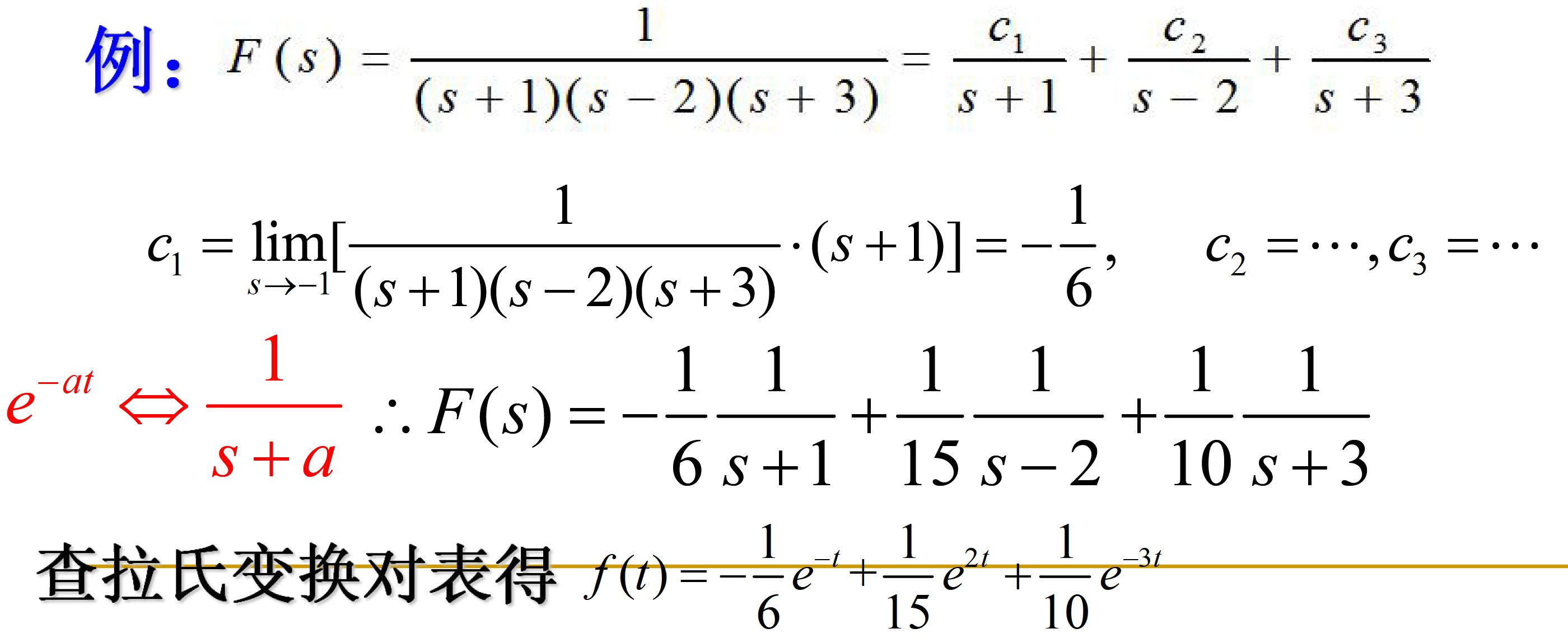
A(s)=0有重根

用拉氏变换求解微分方程

利用拉普拉斯变换法可以方便地求解线性定常系数微分方程，其步骤如下：

1. 对微分方程进行拉普拉斯变换。得到关于s的代数方程。
2. 根据得到的代数方程，求出象函数F(s)的拉普拉斯变换表达式。
3. 将F(s)的拉普拉斯变换展开成部分分式。
4. 查拉普拉斯变换表，求得原函数。