2/6 控制系统的数学模型(下)
控制系统的复域数学模型
传递函数是在对微分方程进行拉普拉斯变换基础上得到的复数域中的数学模型。传递函数不仅可以表征系统的动态特性,而且可以用来研究系统的结构或参数变化对系统性能的影响。经典控制理论中广泛应用的根轨迹法和频域法,就是以传递函数为基础建立起来的,因此,传递函数是经典控制理论中最法本也是最重要的数学模型。
传递函数
定义:注意零初始条件

性质

常用表示形式


注意传递系数和系统增益的概念!

极点和零点对输出的影响
零点:传递函数分子多项式(即输出)等于0的根
极点:传递函数分母多项式(即输入)等于0的根
1, 极点决定了系统自由(固有)运动属性
实数单根、实数复根、共轭复数根、复数重根会分别对应不同的形态,根据极点的种类,自由运动的模态形式将是上述几种形式的线性组合
2, 极点位置决定了系统响应的稳定性和快速性
(1)极点实部的负或正,决定系统是否稳定。全负则稳定,否则不稳定。
(2)极点实部的幅值(极点距离虚轴的位置)决定系统响应的快速性。
3, 零点决定了运动模态的比例
零点决定了各模态在响应中所占的“比例”,因而,也就影响系统响应曲线的形状,影响系统响应的快速性。从工程的角度来看,决不能认为系统的动态性质唯一地由或主要地由传递函数的极点决定,必须注意到零点的作用。
一般来讲,零点离极点较远时,相应于该极点模态所占的比例较大;离极点较近时, 相应于该极点模态所占的比例较小。当零点与极点重合,出现零极点对消现象,此时,相应于该极点的模态也就消失了(实际上是该模态的比例为零)。因此,零点有阻断极点模态“产生”的作用。
结构图
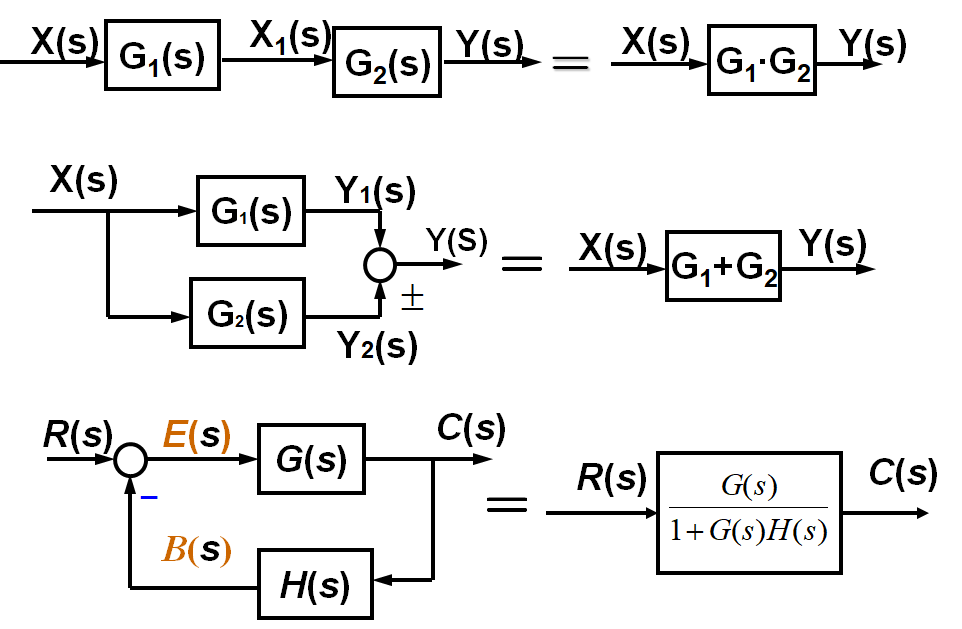
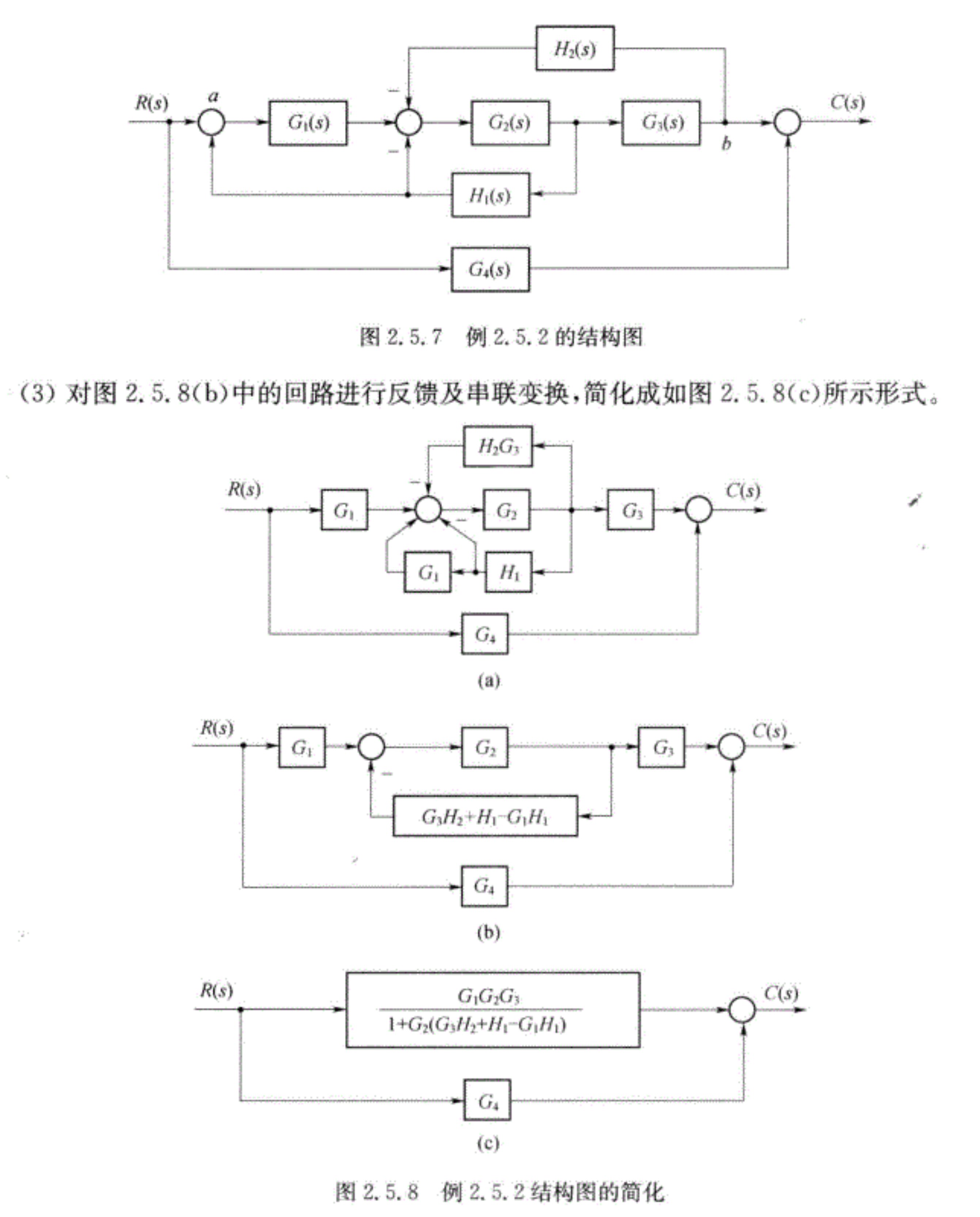
系统的结构图是描述系统各组成元件之间信号传递关系的数学图形。在系统方块图中将方框对应的元部件名称换成其相应的传递函数,并将环节的输入、输出改用拉普拉斯变换表示后,就转换成了相应的系统结构图。

信号流图
信号流图是表示线性代数方程组的示意图,采用信号流图可以直接对代数方程组求解。在控制工程中,信号流图和结构图一样,可用以表示系统的结构及变量传递过程中的数学关系。由于它的符号简单、便于绘制,而且可以通过梅森公式(不必经过图形简化)直接求得系统的传递函数,因此特别适合对于复杂结构系统的分析。
节点:表示系统中的信号,用“⚪”表示,同时具有叠加的作用。支路:连结两个节点的有向线段,表示了一个信号对另一个信号的函数关系,用增益或传递函数表示(相当于乘法器)。
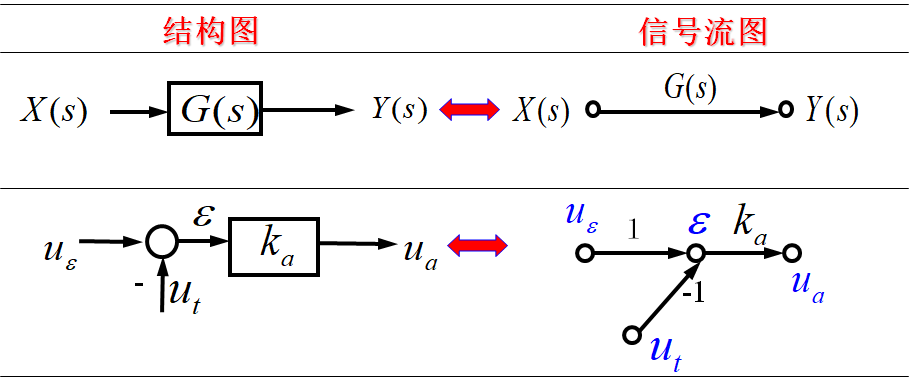
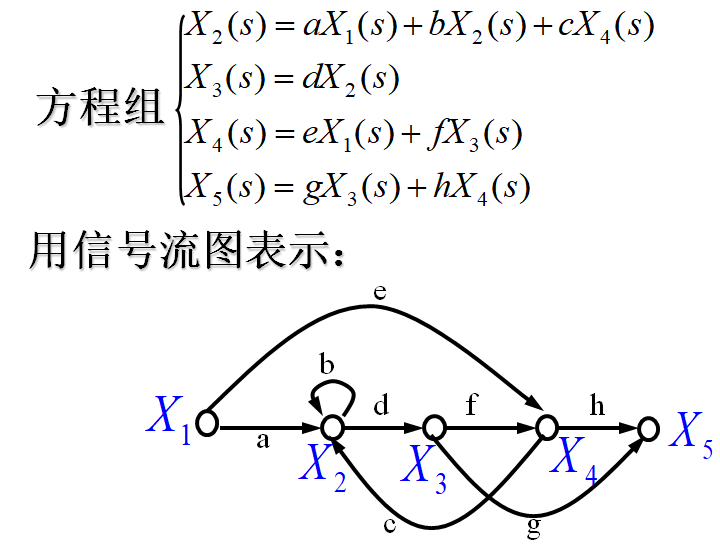
名词术语:源节点(输入节点)、阱节点(输出节点)、混合节点、前向通路、回路、互不接触回路
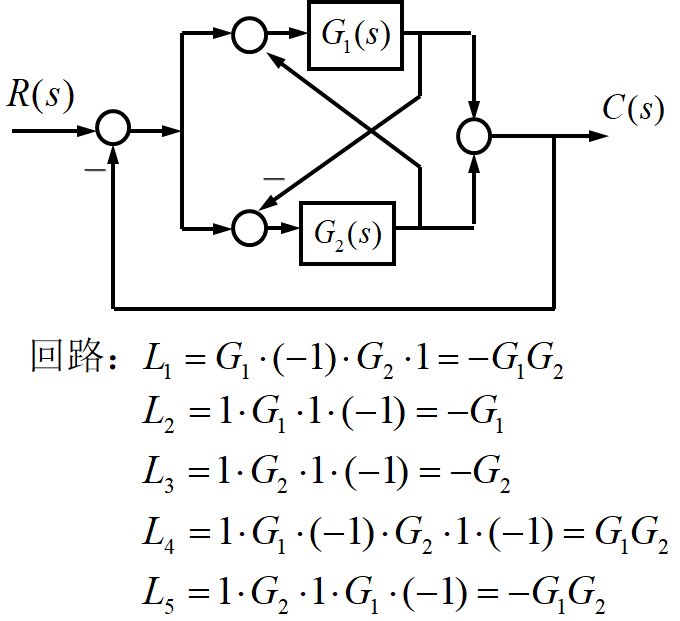
梅森增益公式(对比等效变换理解)

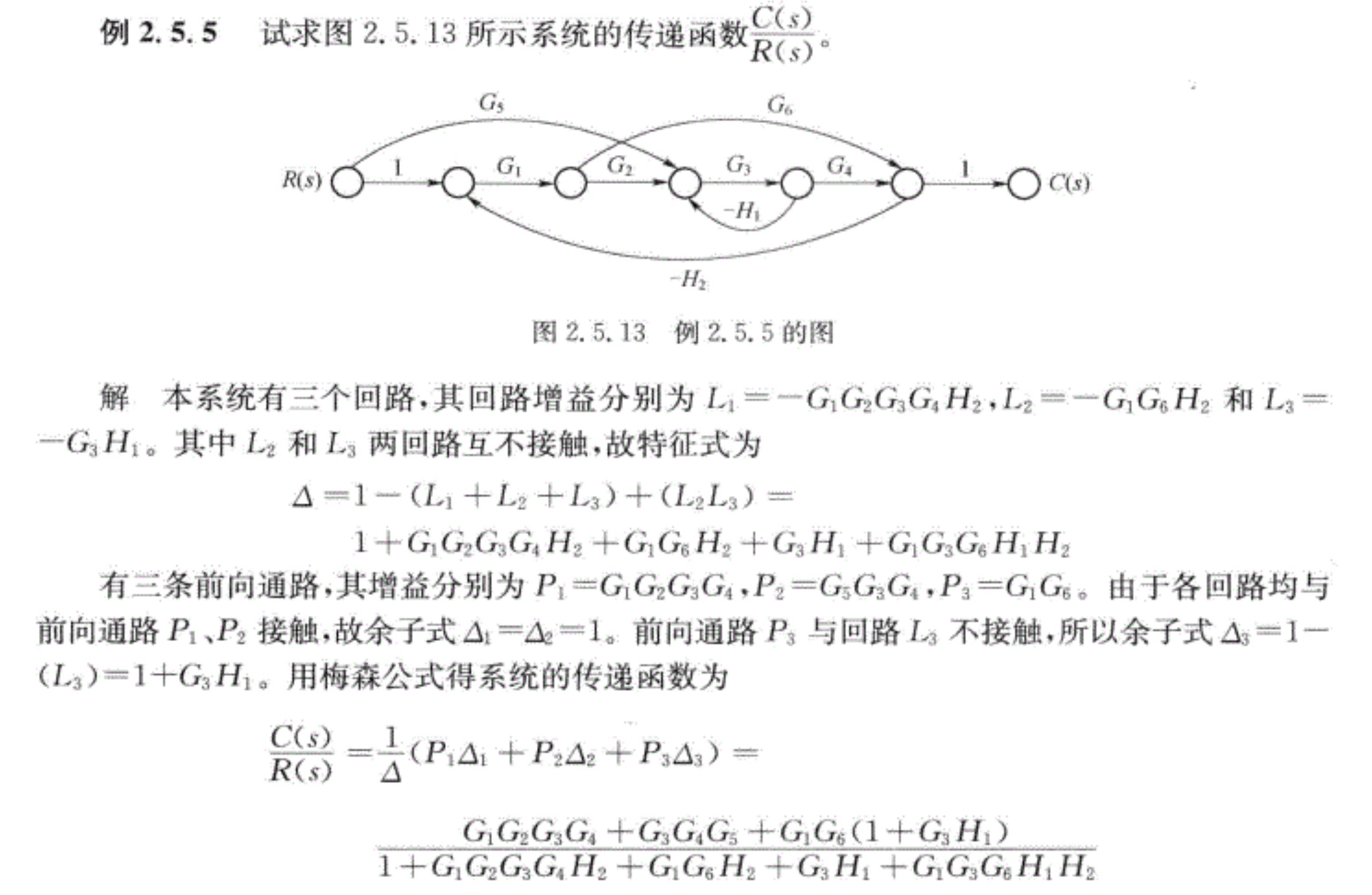
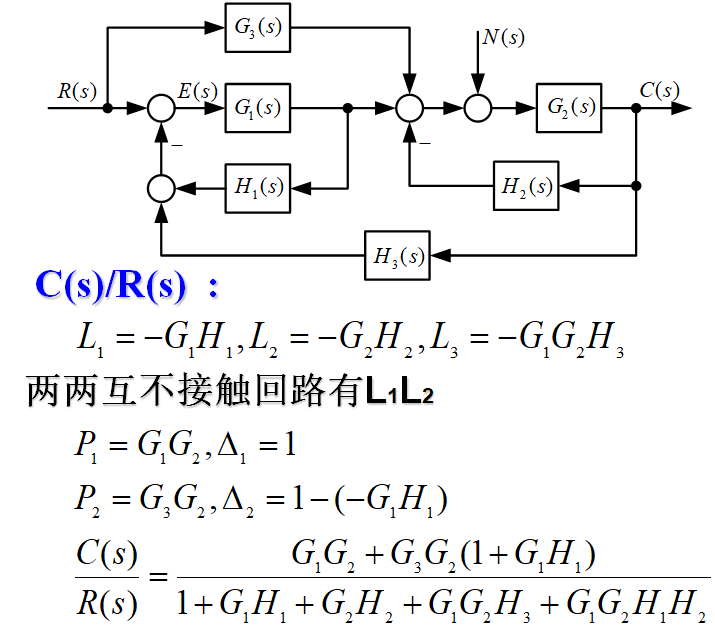
闭环系统的传递函数
实际的控制系统不仅会受到控制输入信号的作用,还会受到干扰信号的作用。下图是具有扰动作用的闭环系统,图中R(s)表示控制输入信号,N(s)表示干扰信号,C(s)代表系统的输出,E(s)代表偏差信号。若将R和N分别看作系统的外作用,C和E看做系统的输出,则该闭环系统就成为一个双输入、双输出系统。
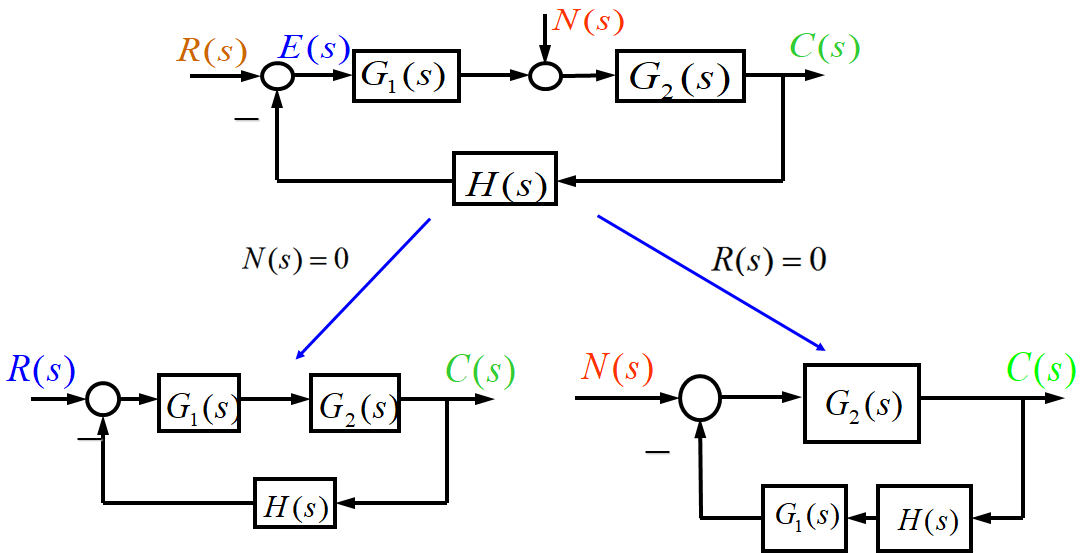
对于上述的闭环系统,可以采用下面的方程组进行描述:
当只研究系统控制输入作用时,令N(s)=0,消去方程组中的E(s),可以求出闭环传递函数为:
当只研究系统在扰动输入作用时,令R(s)=0,消去方程组中的E(s),可求得输出对扰动作用的闭环传递函数为:
当只研究系统控制输入作用时,令N(s)=0,消去方程组中的C(s),可以求出系统的误差传递函数为:
当只研究系统在扰动输入作用时,令R(s)=0,消去方程组中的C(s),可以求出误差对扰动作用的闭环传递函数,简称扰动误差传递函数。
当需要综合考虑时,叠加即可:


