本章首先介绍控制系统的频率特性的基本概念,并建立系统频率特性函数,然后研究用伯德图、奈奎斯特图,尼科尔斯图等图解方法来表示频率特性函数。在讨论了各种典型环节和系统的频率特性后,着重研究利用奈奎斯特稳定性判据和对数稳态判据进行系统稳定性能分析。本章还简要分析了开环系统频率特性与闭环系统频率特性的关系,以及它们与系统时域性能指标的关系;介绍了反馈控制系统的频域校正方法。最后,本章以一个高速列车倾斜控制系统为例,用频率法进行了分析和设计。
引言
本章将研究系统在正弦信号输入下的稳态响应。实验和数学推导都表明,当输入是正弦信号时,线性定常系统的稳态输出也是正弦信号,输出信号的频率与输入信号频率相同,其幅值和相角则是该频率的函数。即输入信号的频率发生变化时,系统稳态响应的幅值和相角变化情况,这也就是系统的频率特性。相应的分析方法,称为系统的频域分析法。主要采用图解。
与其他方法相比较,频率分析法具有如下特点:
- 频率特性可以由前述传递函数确定,也可以用实验的方法来确定,对于难以列写微分方程式的元部件或系统,它便于工程上的使用。
- 频率响应法
借助开环频率特性的图形对系统进行分析,因而具有形象、直观和计算量较少的特点。
- 频率特性有明确的物理意义。对于二阶系统,频域性能指标与时域性能指标有确定的对应关系;对于高阶系统,两者间也存在着近似的对应关系,所以可以把系统参数和结构的变化与动态过程时域指标联系起来。
- 频域分析法不仅可以分析动态性能,而且可以兼顾抑制系统噪声。不仅适用于线性定常系统,而且还可推广到传递函数不是有理数的纯滞后系统,甚至应用到某些非线性系统中。
最后回顾一下复变函数的欧拉方程:
eix=cosx+isinx
频率特性
基本概念
系统的频率响应,是指输入为正弦信号情况下的系统稳态响应。考虑线性系统,其传递函数为Φ(s)。输入为r(t)=Asin(wt+φ),即
R(s)=s2+ω2A(ωcosϕ+ssinϕ)
假设系统稳定且有n个不同的极点p_i,则
Φ(s)=N(s)M(s)=∏i=1n(s−pi)M(s)
则输出C(s)可用部分分式法展开得
C(s)=s−p1k1+s−p2k2+⋯+s−pnkn+s2+ω2αs+βc(s)=k1ep1t+k2ep2t+⋯+knepnt+L−1{s2+ω2αs+β}
式中,α、β为与系统参数与输入相关的常数。如果系统是稳定的,则所有的pi都具有负实部,于是有
t→∞lim(kiepit)=0t→∞limc(t)=L−1{s2+ω2αs+β}=Acsin(ωt+ϕc)
可见,c(t)稳态时为正弦信号,且输入频率与输入信号频率相同。α、β、A_c和\phi_c都与系统参数和输入相关。下面推导幅值和相角的表达式。用s=jw代换传递函数时,多项式中s的偶次方项变换成实部,奇次方项变换为虚部。a,c为偶次方项,b,d为奇次方项。
Cs(s)cs(t)Φ(jω)=c(ω)+jd(ω)a(ω)+jb(ω)=∣Φ(jω)∣ej∠Φ(jω)Φ(−jω)=c(ω)−jd(ω)a(ω)−jb(ω)=∣Φ(jω)∣e−j∠Φ(jω)∣Φ(jω)∣=(c2(ω)+d2(ω)a2(ω)+b2(ω))1/2∠Φ(jω)=arctana(ω)c(ω)+d(ω)b(ω)b(ω)c(ω)−a(ω)d(ω)=s2+ω2αs+β=s+jω1[(s+jω)Φ(s)R(s)∣s=−jω]+s−jω1[(s−jω)Φ(s)R(s)∣s=jω]=s+jωA∣Φ(jω)∣−2je−j(ϕ+∠Φ(jω))+s−jωA∣Φ(jω)∣2jej(ϕ+∠Φ(jω))=A∣Φ(jω)∣2jej(ϕ+∠Φ(jω))−e−j(ϕ+∠Φ(jω))=A∣Φ(jω)∣sin(ωt+ϕ+∠Φ(jω))
综上,得到幅值和相角的表达式为:
{Ac=A∣Φ(jω)∣ϕc=ϕ+∠Φ(jω)
定义输出信号与输入信号的幅值之比A(w),相位之差φ(w)为相频特性,即
⎩⎨⎧A(ω)=Ac/A=∣Φ(jω)∣ϕ(ω)=ϕc−ϕ=∠Φ(jω)Φ(jω)=A(ω)ejϕ(ω)
上述频率特性的定义,既可用于稳定系统,也可适用于不稳定系统。稳定系统的频率特性可以用实验方法确定,即在系统的输入端分别施加不同频率的正弦信号,然后测量系统稳态输出,再根据幅值比和相位差确定系统的频率特性。而对于不稳定系统,由于输出响应的稳态难以测量,所以不能通过实验方法来确定。
通过以上分析可知,频率特性表示了系统或环节对不同频率正弦信号的“跟踪”或“复现”能力,是线性系统在正弦输入信号作用下的稳态输出与输入之比,所以频率特性又叫正弦传递函数。它和传递函数、微分方程一样能反映系统的运动规律,因而它是线性系统(或部件)的又一形式的数学模型。而且频率特性与系统传递函数间的转化也较容易,只要用jw替换复变量s,就能由传递函数Φ(s)直接得到系统的频率特性函数Φ(jw)。三种描述方法间的关系可用下图说明。
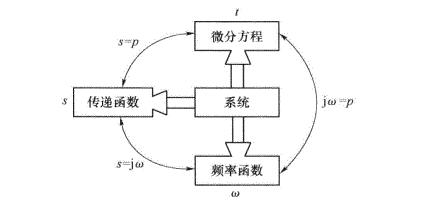

频率特性的集合表示方法
奈奎斯特图
对于任一给定的频率w,频率特性为一复数,在复数平面上表示成一个点。当w从负无穷到正无穷连续变化时,频率特性可表示成一条连续曲线。该曲线就称为奈奎斯特图(简称奈氏图或奈奎斯特曲线),也称为幅相频率特性曲线(简称幅相曲线)。
令X(ω)A(ω)ϕ(ω)=Re[Φ(jω)];Y(ω)=Im[Φ(jω)]=∣Φ(jω)∣=(X2(ω)+Y2(ω))1/2=∠Φ(jω)=arctanX(ω)Y(ω)
由于幅频特性为参变量频率w的偶函数,相频特性为w的奇函数,则w从0变化至+∞和从0变化至-∞这两段关于实轴对称,因此,一般只绘制w从0变化至+∞段的奈奎斯特曲线。并且,在曲线中,用箭头表示w增大时奈奎斯特曲线的变化方向。

伯德图
系统频率特性函数,可以分成幅频特性和相频特性两个函数。因此,可以分别绘制成幅值-频率特性曲线(简称幅频曲线)和相位-频率特性曲线(简称相频曲线)两条曲线.
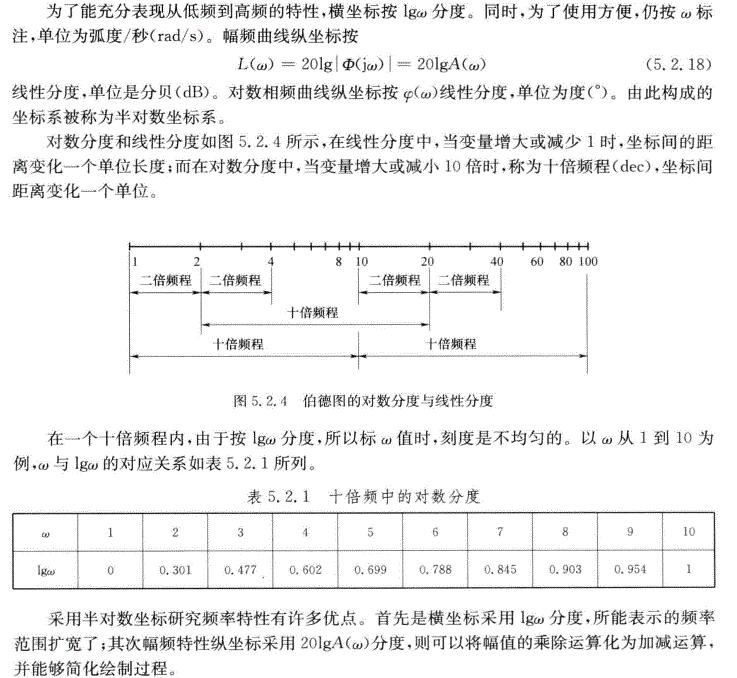
*尼柯尔斯图
开环系统的频率特性
典型环节的频率特性
控制系统种类繁多,但从它们传递函数的形式来看,任何复杂的传递函数,都是由形式有限的典型环节组成。研究这些典型环节的频率特性,有助于我们掌握各种系统的频率特性。线性系统的开环传递函数的分子、分母为实系数多项式,在实系数范围内对它们进行因式分解,一般情况下,可以写成:
G(s)H(s)=sν∏m=1M(Tms+1)∏k=1N(ωk2s2+ωk2ζks+1)K∏i=1Q(τis+1)∏j=1R(ωj2s2+ωj2ζjs+1)

典型环节并不一定和单个元件一一对应,一个元件可能要用多个典型环节表示,而一个典型环节也许是表示多个元件。
知识补充
在以下硬核内容开始前,补充一些三角函数变换的知识:
sin(A±B)=sinAcosB±cosAsinBcos(A±B)=cosAcosB∓sinAsinBtan(A+B)=1−tanAtanBtanA+tanBtan(arctana+arctanb)=1−aba+barctana+arctanb=arctan1−aba+b
比例环节

积分和微分环节

惯性环节和一阶微分环节

振荡环节和二阶微分环节

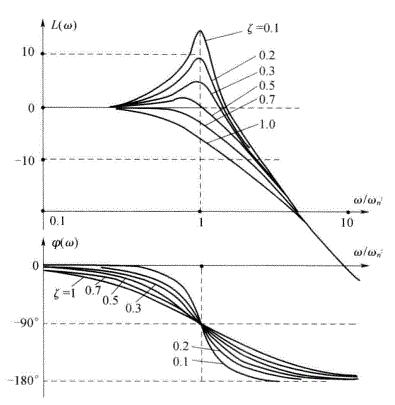

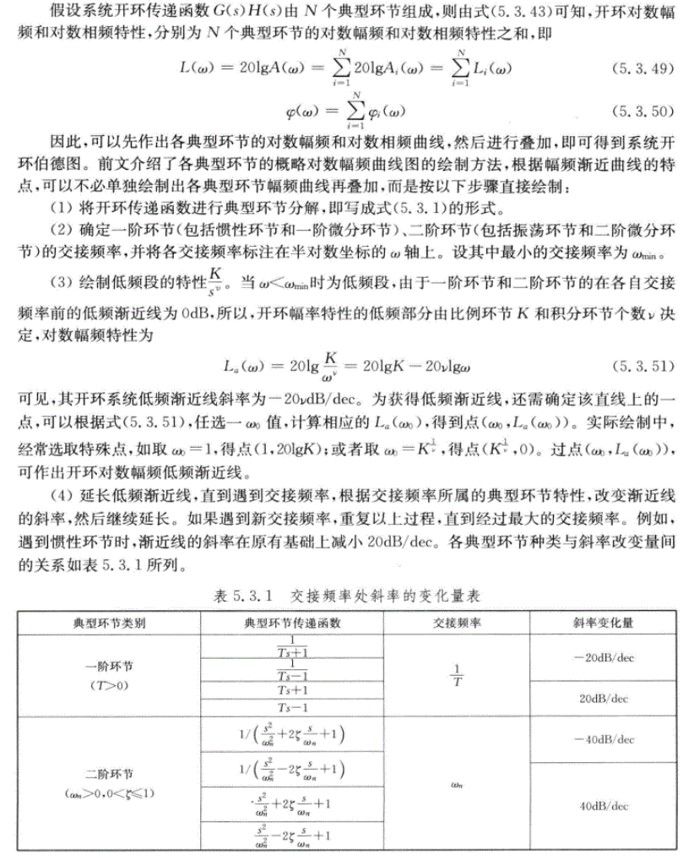
对数幅频渐近特性曲线
工程上常用渐近线近似表示对数频率特性曲线,称为对数幅频渐进特性曲线。惯性环节的对数幅频曲线为:
L(ω)=20lgA(ω)=−20lgT2ω2+1La={0−20lgωT当wT<<1当wT>>1
两线段相交于横坐标\omega=1/T处,此处成为交接频率或转折频率。
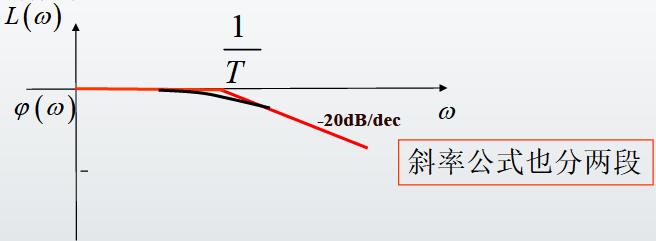
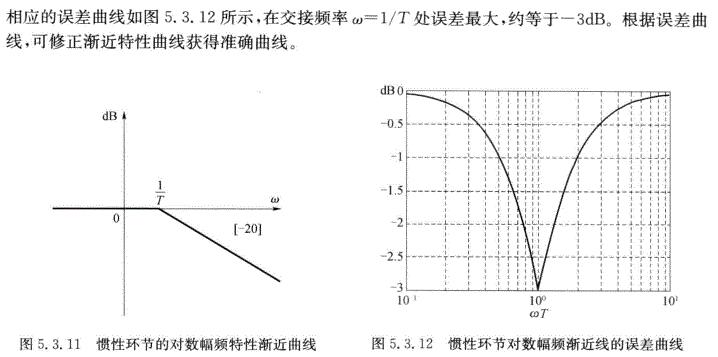
用渐近线表示对数幅频特性时,将会存在误差,即
ΔL(ω)=L(ω)−La(ω)
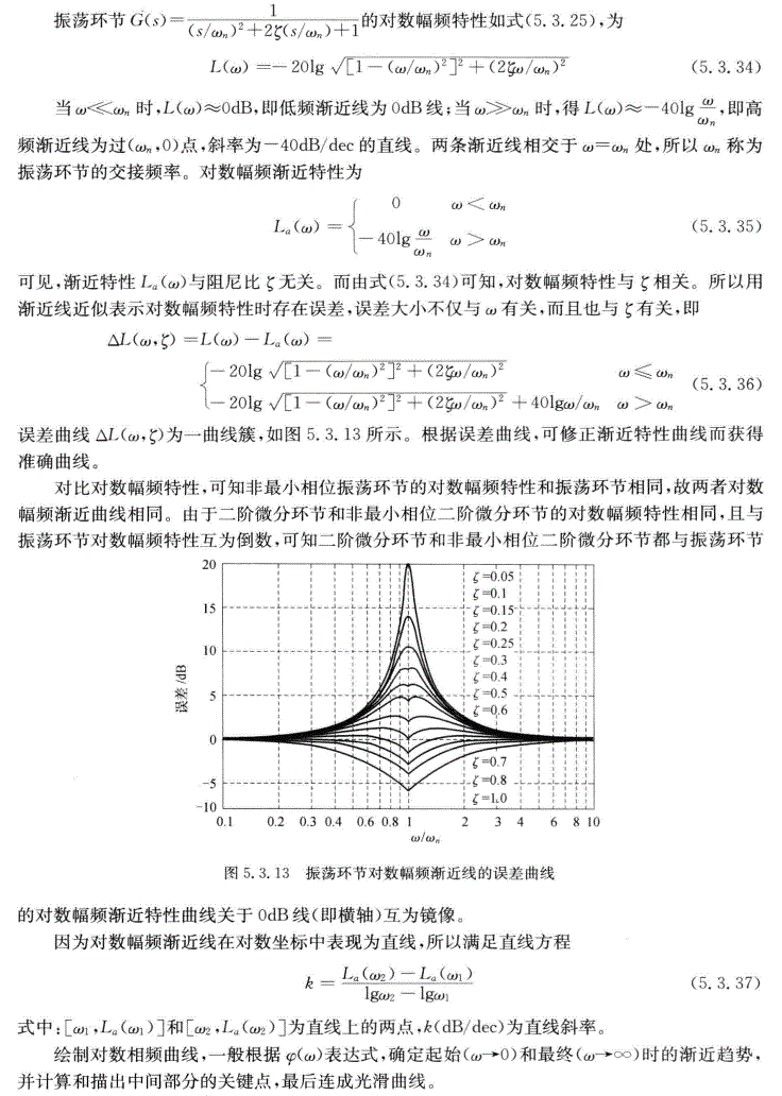
非最小相位环节/不稳定环节
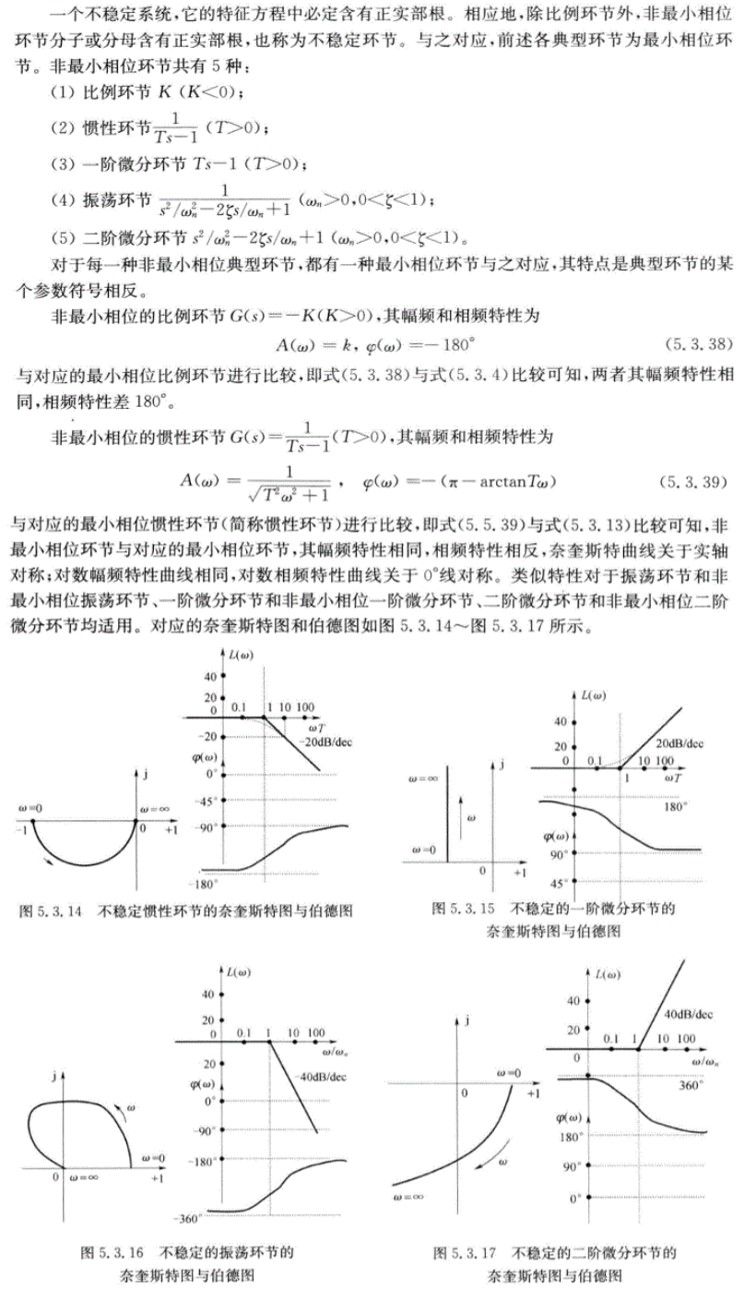
开环系统的频率特性
开环奈奎斯特曲线的绘制



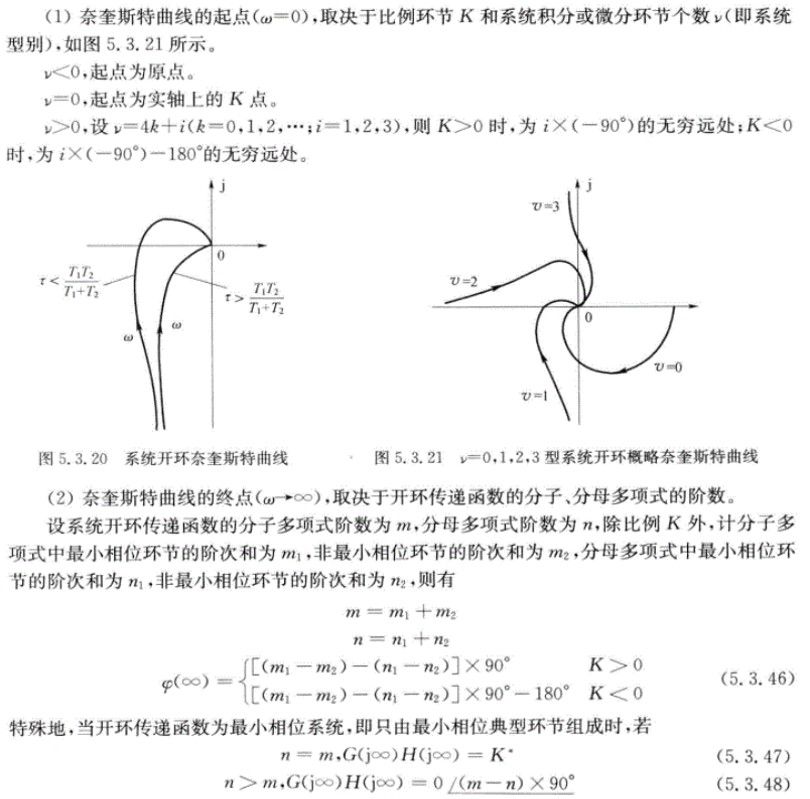
开环伯德图的绘制
tip1:判断各个典型环节的时候并不需要像时域分析法中一样在意"分子"还是“分母”,都应当考虑;
tip2:应当首先将频率函数化成典型环节形式(“尾1”),方便计算各个交接频率;

延迟环节和延迟系统
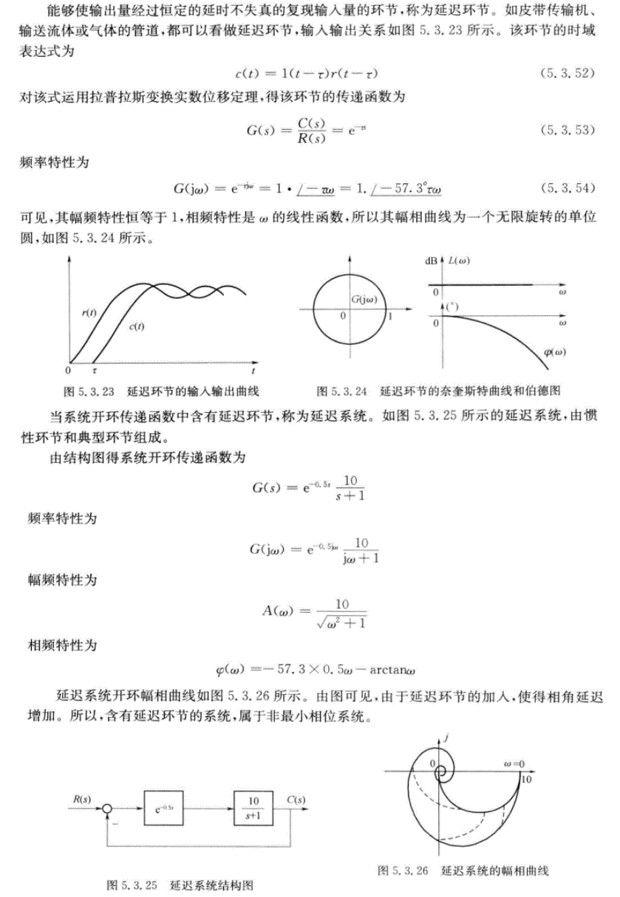
传递函数的频域实验确定



























