数据操作
N维数组是机器学习和神经网络的主要数据结构;
创建数组需要:形状,元素类型,元素的值;
访问的时候可以从一个元素开始、一行一列、子区域,甚至是带步长的分离区域。
连结,Concatenate
我们也可以把多个张量连结(concatenate)在一起, 把它们端对端地叠起来形成一个更大的张量。 我们只需要提供张量列表,并给出沿哪个轴连结。 下面的例子分别演示了当我们沿行(轴-0,形状的第一个元素) 和按列(轴-1,形状的第二个元素)连结两个矩阵时,会发生什么情况。 我们可以看到,第一个输出张量的轴-0长度( 6 )是两个输入张量轴-0长度的总和( 3+3 ); 第二个输出张量的轴-1长度( 8 )是两个输入张量轴-1长度的总和( 4+4 )。
1 2 3 4 5 6 7 8 9 10 11 12 13 X = torch.arange(12 , dtype=torch.float32).reshape((3 ,4 )) Y = torch.tensor([[2.0 , 1 , 4 , 3 ], [1 , 2 , 3 , 4 ], [4 , 3 , 2 , 1 ]]) torch.cat((X, Y), dim=0 ), torch.cat((X, Y), dim=1 ) (tensor([[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [ 8. , 9. , 10. , 11. ], [ 2. , 1. , 4. , 3. ], [ 1. , 2. , 3. , 4. ], [ 4. , 3. , 2. , 1. ]]), tensor([[ 0. , 1. , 2. , 3. , 2. , 1. , 4. , 3. ], [ 4. , 5. , 6. , 7. , 1. , 2. , 3. , 4. ], [ 8. , 9. , 10. , 11. , 4. , 3. , 2. , 1. ]]))
广播机制
在上面的部分中,我们看到了如何在相同形状的两个张量上执行按元素操作。 在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作。 这种机制的工作方式如下:首先,通过适当复制元素来扩展一个或两个数组, 以便在转换之后,两个张量具有相同的形状。 其次,对生成的数组执行按元素操作。
1 2 3 4 5 6 7 8 9 10 11 a = torch.arange(3 ).reshape((3 , 1 )) b = torch.arange(2 ).reshape((1 , 2 )) a, b, a+b (tensor([[0 ], [1 ], [2 ]]), tensor([[0 , 1 ]]), tensor([[0 , 1 ], [1 , 2 ], [2 , 3 ]]))
索引和切片
就像在任何其他Python数组中一样,张量中的元素可以通过索引访问。 与任何Python数组一样:第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素。
节省内存
运行一些操作可能会导致为新结果分配内存。例如,如果我们用Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
1 2 3 4 5 before = id (Y) Y = Y + X id (Y) == before, before, id (Y)(False , 2153248149728 , 2153248204096 )
这可能是不可取的,原因有两个:首先,我们不想总是不必要地分配内存。 在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。 通常情况下,我们希望原地执行这些更新。 其次,如果我们不原地更新,其他引用仍然会指向旧的内存位置, 这样我们的某些代码可能会无意中引用旧的参数。。 为了说明这一点,我们首先创建一个新的矩阵Z,其形状与另一个Y相同, 使用zeros_like来分配一个全 0 的块。
1 2 3 4 5 6 7 Z = torch.zeros_like(Y) print ('id(Z):' , id (Z))Z[:] = X + Y print ('id(Z):' , id (Z))id (Z): 2153570368624 id (Z): 2153570368624
如果在后续计算中没有重复使用X, 我们也可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
1 2 3 4 5 6 before = id (X) X += Y X[:] = X + Y id (X) == beforeTrue
转换为其他python对象
将深度学习框架定义的张量转换为NumPy张量(ndarray)很容易,反之也同样容易。 torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量。
1 2 3 4 5 6 7 X = torch.arange(12 , dtype=torch.float32).reshape((3 ,4 )) A = X.numpy() B = torch.tensor(A) type (X),type (A), type (B), id (X), id (A), id (B)(torch.Tensor, numpy.ndarray, torch.Tensor, 2153570697440 , 2153570749968 , 2153570698640 )
1 2 3 4 5 6 7 8 9 10 11 12 X[2 ,:] = 36 X, A, B (tensor([[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [36. , 36. , 36. , 36. ]]), array([[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [36. , 36. , 36. , 36. ]], dtype=float32), tensor([[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [ 8. , 9. , 10. , 11. ]]))
1 2 3 4 5 6 7 8 9 10 11 12 A[1 ,:] = 1 X, A, B (tensor([[ 0. , 1. , 2. , 3. ], [ 1. , 1. , 1. , 1. ], [36. , 36. , 36. , 36. ]]), array([[ 0. , 1. , 2. , 3. ], [ 1. , 1. , 1. , 1. ], [36. , 36. , 36. , 36. ]], dtype=float32), tensor([[ 0. , 1. , 2. , 3. ], [ 4. , 5. , 6. , 7. ], [ 8. , 9. , 10. , 11. ]]))
1 2 3 4 5 6 7 8 9 10 11 12 B[0 ,3 ] = 128 X, A, B (tensor([[ 0. , 1. , 2. , 3. ], [ 1. , 1. , 1. , 1. ], [36. , 36. , 36. , 36. ]]), array([[ 0. , 1. , 2. , 3. ], [ 1. , 1. , 1. , 1. ], [36. , 36. , 36. , 36. ]], dtype=float32), tensor([[ 0. , 1. , 2. , 128. ], [ 4. , 5. , 6. , 7. ], [ 8. , 9. , 10. , 11. ]]))
要(将大小为1的张量转换为Python标量),我们可以调用item函数或Python的内置函数。
1 2 3 4 a = torch.tensor([3.5 ]) a, a.item(), float (a), int (a) (tensor([3.5000 ]), 3.5 , 3.5 , 3 )
数据预处理
为了能用深度学习来解决现实世界的问题,我们经常从预处理原始数据开始, 而不是从那些准备好的张量格式数据开始。 在Python中常用的数据分析工具中,我们通常使用pandas软件包。 像庞大的Python生态系统中的许多其他扩展包一样,pandas可以与张量兼容。 本节我们将简要介绍使用pandas预处理原始数据,并将原始数据转换为张量格式的步骤。 我们将在后面的章节中介绍更多的数据预处理技术。
读取数据集
举一个例子,我们首先(创建一个人工数据集,并存储在CSV(逗号分隔值)文件) …/data/house_tiny.csv中。 以其他格式存储的数据也可以通过类似的方式进行处理。 下面我们将数据集按行写入CSV文件中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import osimport pandas as pdos.makedirs(os.path.join('..' , 'data' ), exist_ok=True ) data_file = os.path.join('..' , 'data' , 'house_tiny.csv' ) with open (data_file, 'w' ) as f: f.write('NumRooms,Alley,Price\n' ) f.write('NA,Pave,127500\n' ) f.write('2,NA,106000\n' ) f.write('4,NA,178100\n' ) f.write('NA,NA,140000\n' ) data = pd.read_csv(data_file) print (data) NumRooms Alley Price 0 NaN Pave 127500 1 2.0 NaN 106000 2 4.0 NaN 178100 3 NaN NaN 140000
处理缺失值
为了处理缺失的数据,典型的方法包括插值法和删除法,其中插值法用一个替代值弥补缺失值,而删除法则直接忽略缺失值。 在(这里,我们将考虑插值法)。
1 2 3 4 5 6 7 8 9 inputs, outputs = data.iloc[:, 0 :2 ], data.iloc[:, 2 ] inputs = inputs.fillna(inputs.mean()) print (inputs) NumRooms Alley 0 3.0 Pave1 2.0 NaN2 4.0 NaN3 3.0 NaN
对于inputs中的类别值或离散值,我们将“NaN”视为一个类别。由于“巷子类型”(“Alley”)列只接受两种类型的类别值“Pave”和“NaN”, pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。 巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
1 2 3 4 5 6 7 8 inputs = pd.get_dummies(inputs, dummy_na=True ) print (inputs) NumRooms Alley_Pave Alley_nan 0 3.0 1 0 1 2.0 0 1 2 4.0 0 1 3 3.0 0 1
转换为张量格式
1 2 3 4 5 6 7 8 9 import torchX, y = torch.tensor(inputs.values), torch.tensor(outputs.values) X, y (tensor([[3. , 1. , 0. ], [2. , 0. , 1. ], [4. , 0. , 1. ], [3. , 0. , 1. ]], dtype=torch.float64), tensor([127500 , 106000 , 178100 , 140000 ]))
线性代数
在数学表示法中,将向量记为粗体的小写的符号。而向量的任一元素是标量,不用加粗。
长度,维度和形状
向量只是一个数字数组,就像每个数组都有一个长度一样,每个向量也是如此。在数学表示法中,如果我们想说一个向量x \mathbf{x} x n n n x ∈ R n \mathbf{x}\in\mathbb{R}^n x ∈ R n 维度 (dimension)。len()函数来访问张量的长度。.shape属性访问向量的长度。只有一个轴的张量,形状只有一个元素。 )
1 2 3 4 5 import torchx=torch.arange(4 ) len (x), x.shape4 , torch.Size([4 ])
请注意,维度 (dimension)这个词在不同上下文时往往会有不同的含义,这经常会使人感到困惑。向量 或轴 的维度被用来表示向量 或轴 的长度,即向量或轴的元素数量。
矩阵与张量
正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。矩阵,我们通常用粗体、大写字母来表示(例如,X \mathbf{X} X Y \mathbf{Y} Y Z \mathbf{Z} Z
范数
:label:subsec_lin-algebra-norms
线性代数中最有用的一些运算符是范数 (norm)。非正式地说,一个向量的范数 告诉我们一个向量有多大。这里考虑的大小 (size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数f f f x \mathbf{x} x α \alpha α
f ( α x ) = ∣ α ∣ f ( x ) . f(\alpha \mathbf{x}) = |\alpha| f(\mathbf{x}).
f ( α x ) = ∣ α ∣ f ( x ) .
第二个性质是我们熟悉的三角不等式:
f ( x + y ) ≤ f ( x ) + f ( y ) . f(\mathbf{x} + \mathbf{y}) \leq f(\mathbf{x}) + f(\mathbf{y}).
f ( x + y ) ≤ f ( x ) + f ( y ) .
第三个性质简单地说范数必须是非负的:
f ( x ) ≥ 0. f(\mathbf{x}) \geq 0.
f ( x ) ≥ 0.
这是有道理的。因为在大多数情况下,任何东西的最小的大小是0。
∀ i , [ x ] i = 0 ⇔ f ( x ) = 0. \forall i, [\mathbf{x}]_i = 0 \Leftrightarrow f(\mathbf{x})=0.
∀ i , [ x ] i = 0 ⇔ f ( x ) = 0.
你可能会注意到,范数听起来很像距离的度量。如果你还记得欧几里得距离和毕达哥拉斯定理,那么非负性的概念和三角不等式可能会给你一些启发。事实上,欧几里得距离是一个L 2 L_2 L 2 n n n x \mathbf{x} x x 1 , … , x n x_1,\ldots,x_n x 1 , … , x n L 2 L_2 L 2 范数 是向量元素平方和的平方根:
∥ x ∥ 2 = ∑ i = 1 n x i 2 , \|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2},
∥ x ∥ 2 = i = 1 ∑ n x i 2 ,
其中,在L 2 L_2 L 2 2 2 2 ∥ x ∥ \|\mathbf{x}\| ∥ x ∥ ∥ x ∥ 2 \|\mathbf{x}\|_2 ∥ x ∥ 2 L 2 L_2 L 2
在深度学习中,我们更经常地使用L 2 L_2 L 2 L 1 L_1 L 1
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ . \|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|.
∥ x ∥ 1 = i = 1 ∑ n ∣ x i ∣ .
与L 2 L_2 L 2 L 1 L_1 L 1 L 1 L_1 L 1
L 2 L_2 L 2 L 1 L_1 L 1 L p L_p L p
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 / p . \|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}.
∥ x ∥ p = ( i = 1 ∑ n ∣ x i ∣ p ) 1/ p .
类似于向量的L 2 L_2 L 2 矩阵 ]X ∈ R m × n \mathbf{X} \in \mathbb{R}^{m \times n} X ∈ R m × n 的Frobenius范数 (Frobenius norm)是矩阵元素平方和的平方根: )
∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 . \|\mathbf{X}\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2}.
∥ X ∥ F = i = 1 ∑ m j = 1 ∑ n x ij 2 .
Frobenius范数满足向量范数的所有性质,它就像是矩阵形向量的L 2 L_2 L 2
例题
微积分题
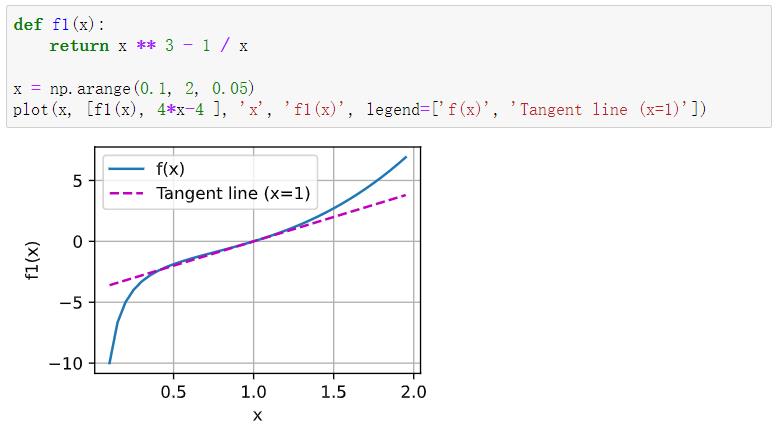
绘制函数y = f ( x ) = x 3 − 1 x y = f(x) = x^3 - \frac{1}{x} y = f ( x ) = x 3 − x 1 x = 1 x = 1 x = 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 %matplotlib inline import numpy as npfrom matplotlib_inline import backend_inlinefrom d2l import torch as d2ldef numerical_lim (f, x, h ): return (f(x + h) - f(x)) / h def use_svg_display (): """使用svg格式在Jupyter中显示绘图""" backend_inline.set_matplotlib_formats('svg' ) def set_figsize (figsize=(3.5 , 2.5 ): """设置matplotlib的图表大小""" use_svg_display() d2l.plt.rcParams['figure.figsize' ] = figsize def set_axes (axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend ): """设置matplotlib的轴""" axes.set_xlabel(xlabel) axes.set_ylabel(ylabel) axes.set_xscale(xscale) axes.set_yscale(yscale) axes.set_xlim(xlim) axes.set_ylim(ylim) if legend: axes.legend(legend) axes.grid() def plot (X, Y=None , xlabel=None , ylabel=None , legend=None , xlim=None , ylim=None , xscale='linear' , yscale='linear' , fmts=('-' , 'm--' , 'g-.' , 'r:' 3.5 , 2.5 None ): """绘制数据点""" if legend is None : legend = [] set_figsize(figsize) axes = axes if axes else d2l.plt.gca() def has_one_axis (X ): return (hasattr (X, "ndim" ) and X.ndim == 1 or isinstance (X, list ) and not hasattr (X[0 ], "__len__" )) if has_one_axis(X): X = [X] if Y is None : X, Y = [[]] * len (X), X elif has_one_axis(Y): Y = [Y] if len (X) != len (Y): X = X * len (Y) axes.cla() for x, y, fmt in zip (X, Y, fmts): if len (x): axes.plot(x, y, fmt) else : axes.plot(y, fmt) set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
自动求导例题
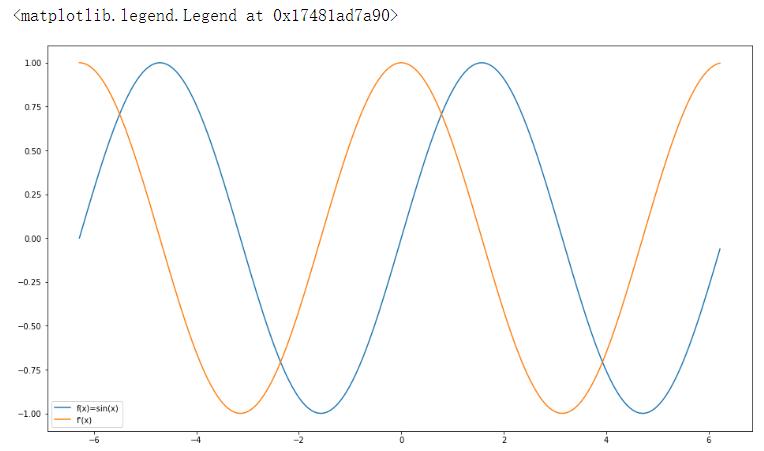
使f ( x ) = sin ( x ) f(x)=\sin(x) f ( x ) = sin ( x ) f ( x ) f(x) f ( x ) d f ( x ) d x \frac{df(x)}{dx} d x df ( x ) f ′ ( x ) = cos ( x ) f'(x)=\cos(x) f ′ ( x ) = cos ( x )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 %matplotlib inline import matplotlibimport matplotlib.pyplot as pltimport torchimport numpy as npt=torch.arange(-2 *np.pi, 2 *np.pi, 0.02 *np.pi, requires_grad=True ) y0=torch.zeros(len (t)) dy=torch.zeros(len (t)) for i in range (len (t)): m=t[i] n=torch.tensor([m]) n.requires_grad_(True ) y=torch.sin(n) y.backward() y0[i]=y dy[i]=n.grad n.grad.zero_() plt.figure(figsize=(16 , 9 )) plt.plot(t.detach().numpy(),y0.detach().numpy(),label='f(x)=sin(x)' ) plt.plot(t.detach().numpy(),dy.detach().numpy(),label="f'(x)" ) plt.legend(loc=0 )